まず半径=1の単位円上では
sinθはy/1でy(縦)
cosθはx/1でx(横)
tanθはy/xでグラフの傾きになる。
微分で求める導関数(二つの点の間隔を極限まで小さくして求めるグラフ)は円の接線になるので、θのグラフと導関数は直角でクロスすることになる(円の接線は円と垂直に接する)。
したがって三角比を微分するとサインとコサインの位置関係が90°ずれるので
sinθ′=cosθ
cosθ′=-sinθ(増減関係がcosθと逆だから※cosの長さは角度が増えると縮む)
さらに
-sinθ′=-cosθ
-cosθ′=sinθ
となり、4回微分すると90°×4で一周してくる。
ちなみにタンジェントの微分だけは図で説明しているテキストがなぜかなくて、サインとコサインは図で表すと割と簡単なんだからタンジェントも行けるだろ、と絵を描いて考えてみました。
確かにサインコサインに比べてちょっと面倒くさいんだけど、中学三年生の相似の知識で行けるし、私みたいなのはビジュアルがないときついのでレッツ正接。
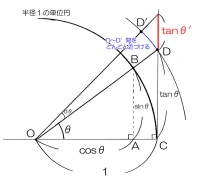
まずタンジェントの微分(tanθ′)の位置を確認。タンジェントは単位円上では底辺1の直角三角形の高さを担当するので、赤い線のあそこになります。
△OABと△OCDは相似なので
OB:OD=OA:OC
1:X=cosθ:1
cosθX=1
X=1/cosθ
よって
OD=1/cosθ
次に図のD~D′のディファレンチエーションしてるところをクローズアップする。
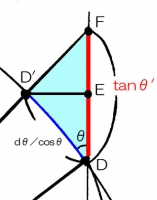
最初の図の△OCDと、クローズアップした図の△DED′は相似なので
ODとDD′は対応している。
よって
OD=1/cosθから
DD′は1/cosθの微分
DD′=dθ/cosθ
さらに△OCD∽△DD′Fでもあるので
OD:DF=OC:DD′
1/cosθ:tanθ′=1:dθ/cosθ
tanθ′=(1/cosθ)×(dθ/cosθ)
tanθ′=dθ/cosθ²
よって
tanθ′=1/cosθ²
まとめ
sinθ′=cosθ
cosθ′=-sinθ
tanθ′=1/cosθ²
ちなみに
サインの逆数をコセカント(cosec)
コサインの逆数をセカント(sec)
タンジェントの逆数をコタンジェント(cot)
という。
よって
tanθ′=1/cosθ²=secθ²
また三平方の定理より
sinθ²+cosθ²=1
各項をcos²で割ると
sinθ²/cosθ²+cosθ²/cosθ²=1/ cosθ²
sinθ/cosθ=tanθより
tan θ²+1=1/ cosθ²
というわけで
tanθ′=tanθ ²+1