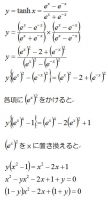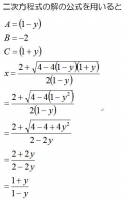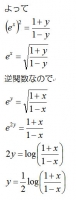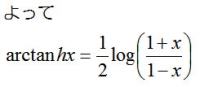まずはこちらをご覧いただきたい。
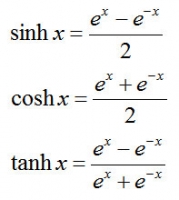
こんな感じの関数三兄弟を双曲線関数といい、三角関数のようにハイパボリックサイン、ハイパボリックコサイン、ハイパボリックタンジェントと名前がついている(ハイパボリックはハイ・パラボラで双曲線という意味)。
y=sinθとx=cosθの座標が半径1の円周上(x²+y²=1)の点に対応しているように、双曲線関数y=sinhθとx=coshθの座標は双曲線上(x²-y²=1)の点に対応している。また、計算上の性質も三角関数に似ている。
ちなみに、グラフの形自体は(サイン、コサインのグラフがパルス状で円形でないのと同様に)、両端を固定されたロープがたわんだような形で双曲線ではない。
さらに、双曲線関数はこんなふうに定義がいきなり出てくるんだけど、なんでこういう式になったかの証明は難関大学レベルらしいのでスルーの方向でお願いします。※オイラーの公式で出せるらしい。
ハイパボリックサインの逆関数

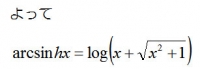
ハイパボリックコサインの逆関数

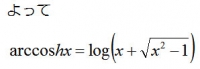
ハイパボリックタンジェントの逆関数