しかし、『真田丸』見てても思うけど、時代の変わり目に生まれちゃった人って大変だよな。子どもの頃に前時代の価値観を教育されたのに、その価値観がもはや通用しない時代を大人になって生きなきゃいけなかったわけで。そういう葛藤や悲哀をやりたかったんだろうけど、やっぱり『真田丸』みたいな上手なドラマ見ちゃうと、この映画のイドリス・エルバさんももうちょっと上手く描けたんじゃないかなとは思う。前作の敵の存在感が非常に強烈だっただけにね。
人を殺して生きるなら死んだほうがマシだ。そういう時代に生まれた。
合成関数の微分
複雑な式yをxで微分する場合は、その式を一度、ひとつの文字(例えばu)に置き換えてから、微分を行う。
しかしその場合は、yをuで微分したことになっちゃうのでuをさらにxで微分しなければならない。
そのためには、yをuで微分した答えと、uをxで微分した答えをかければ、uが消えてくれるので
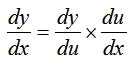
となる。
例題


分数の対数関数の微分
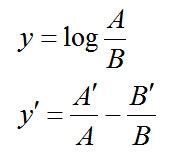
例題1
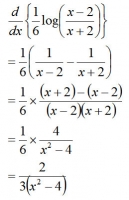
例題2

極方程式
極座標(原点からの距離rと角度θを表す座標)による方程式
r=cosθ
を直交座標に直す。
直交座標(普通の座標)では
①x(幅)=rcosθ
②y(高さ)=rsinθ
③x²+y²=r²(円の方程式)
なので
r=cosθの両辺にrをかけると
r²=rcosθ
①と③を代入して
x²+y²=x
移項して
x²-x+y²=0
x²-xの部分を平方完成して
(x-1/2)²+y²=1/4
この円の方程式は
x座標が1/2
y座標が0
r²=1/4なので半径rは1/2
の円を示す。
ロピタルの定理
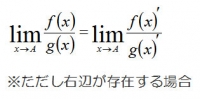
例題1

例題2
