金属の熱伝導率の測定
熱の伝わり方が金属の種類によってそれぞれ異なることを確かめる実験。L字型に成型された金属の棒を懐かしのアルコールランプで端から熱し、もう一方の端に取り付けた蝋が溶けるタイムを競い合う。
また、その結果を踏まえて、金属の中を熱が伝わる過程や、金属の種類によって熱の伝わる速さが異なる原因を解明する。
実験に用いる試料は、銅(Cu)、アルミニウム(Al)、鉄(Fe)、真鍮(Cu-Zn合金)の4種類である。
実験方法
1.試料台加熱部はくぼんだ部分を下にしてスタンドに固定する。
2.L型試料棒を上向きに、試料台加熱部の穴に押し込んでしっかり固定する。
3.ステンレスのリングを試料棒の上端から1mm~2mmのところにピンセットを用いてささえ、ろうそくのろうをリングの内側に流し込んでリングを固定する。この時のろうのつけ具合で測定値に誤差が生じる恐れがあるので十分注意すること。
4.アルコールランプに点火し、炎が試料台加熱部のくぼみに当たるように位置や高さを調節する。この時注意することは炎が外的要因によって曲がったり安定しない場合は、その影響を取り除く努力が必要である。
5.だいたい2~10分で銅、アルミニウム、真鍮、鉄の順にリングが降下する。炎が試料台加熱部のくぼみに当てたときからリングが落ちるまでの時間をストップウォッチで測定する。(集中していないと値に誤差を生む要因となりうるので注意すること)
6.測定データの整理は6回測定して上限と下限の値をカットして、残ったデータの平均を取るのが一般的である。
金属中に熱が伝わる時間と熱伝導率の関係
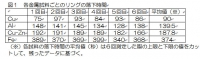
4種類の試料におけるリングの落下時間について、測定回数ごとに表に整理すると同時に、その平均値を求めた(図1)。
図1 各試料ごとのリングの落下時間
マスターカーブ
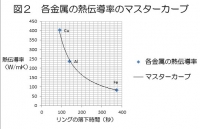
次に、あらゆる金属の熱伝導率と熱の伝わる時間との関係をグラフに描いた(図2)。
今回測定した3つの単一金属の測定点を通る線がマスターカーブ(太線)である。このカーブの意味は、金属合金の熱伝導率と熱の伝わる時間との関係は、ほとんどの場合、この線上のどこかにプロットされるということである。
図2 各金属のマスターカーブ
合金の成分の求め方
加熱時間を横軸に、それぞれの試料棒の熱伝導率を縦軸にとった、銅(Cu)、アルミニウム(Al)、鉄(Fe)の純金属によるマスターカーブを基に、真鍮(Cu-Zn合金)の熱伝導率を求め、そこに含まれる単一金属の割合を求めた。
それぞれの金属の熱伝導率は
Cuが403(W/mK)
Alが236(W/mK)
Feが83.5(W/mK)
Znが121(W/mK)
である。
真鍮(Cu-Zn)の熱伝導率を、図2のマスターカーブに実験で測定した落下時間の187.8秒を代入することで求めると、その値は約185(W/mK)となる。
この熱伝導率の値から、実験で用いた真鍮に含まれる銅と亜鉛の割合を求めると、以下の式で表すことができる。
X=XA×a+XB×b・・・(1)
Xは合金の熱伝導率
XAは単一金属Aの熱伝導率
aは単一金属Aの含有率(%)
XBは単一金属Bの熱伝導率
bは単一金属Bの含有率(%) をそれぞれ表す。
金属の熱の伝わり方は電気の伝わり方と同じ原理であるため、式(1)は、異なる熱伝導率を持つ単一金属を混ぜた合金を、ある種の直列回路とみなしている。
したがって、直列回路全体の電流は各回路の電流の和となることから、合金全体の熱伝導率は、それぞれの単一金属の熱伝導率の和と考えることができる。
この式(1)を用いて、単一金属Aを銅、単一金属Bを亜鉛として、銅の含有率aを求めた。
銅の熱伝導率は403
亜鉛の熱伝導率は121
真鍮の伝導率は185
なので・・・
185=403×(a/100)+121×(100-a/100)
a=22.7(%)
b=100-aよりb=77.3(%)
よって実験で用いた真鍮は銅が22.7%、亜鉛が77.3%含まれていることがわかった。
合金の熱伝導率の求め方
さっきの逆パターンと考える。
今度は式(1)に、合金に混ぜた単一金属Aの割合(%)と、合金に混ぜた単一金属Bの割合b(%)を代入すれば、合金の熱伝導率が求められる。
フーリエの法則
実験では導電性が高い銅の熱伝導率が高く、導電性の低い鉄の熱伝導率が低いことから、電気と熱は同じメカニズムで伝わっていることがわかった。
つまり、電圧が2つの電極の電位差が大きいほど大きくなることと同様に、熱量Iは2つの物体間の温度勾配が大きいほど大きくなる(フーリエの法則)。したがって熱伝導率kは、同じ熱量が発生した場合は、温度勾配が小さいほど大きく、温度勾配が大きいほど小さい。
k=ID/T2-T1・・・(2)
kは熱伝導率
Iは熱量
Dは金属棒の直径(断面積の大きさ)
(T1-T2)は温度勾配 をそれぞれ表す。
これも電力(W)を電圧(V)で割れば、電流(A)の値(=電気抵抗の値≒電気伝導率ρ※)が求められることと同じである。
(※)電気伝導率は電気抵抗の逆数である。