ぐんまけん!には向井千秋記念館という科学館がある。そこに高さは同じだけれど角度が異なる2つのスロープに金属球を転がせて、どっちの球が先にゴールするか実験してみよう!みたいな装置があるんだけど、キャプションに正解とか原理がなくて、問題の出し方的に、おそらく高さが同じところから転がすわけだから、位置エネルギーは一緒で同時ゴールなのかなって思ってたら、もうダントツで角度が急なスロープの方が緩やかなスロープよりも距離が長いのにタイムが早いんだよね。
で、なんでなんだろうって学芸員さんに聞いたら、この装置は寄贈なのでオレもそもそも何を伝えたいかよくわからないみたいな衝撃的な返答が返ってきて、ますます謎が深まったんだけど、今回その謎がついに明らかにされました。
今回の実験では、このような二つのコースで金属球のゴールするタイムを比較した。
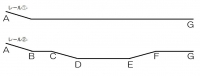
この実験で使うのは中学三年生で習う、力学的エネルギー保存の法則オンリー。これについての詳細はリンク先で。
レール①
①スタート後B地点ではA地点とB地点の位置エネルギー差が運動エネルギーとなり速度Bを持つ。その速度を求める。
力学的エネルギー保存の法則により
A地点の位置エネルギー=B地点の位置エネルギー+B地点の運動エネルギー
※A地点では金属球は静止しているので運動エネルギー=0とする。
mghA=mghB+1/2mv2 ・・・(1)
なので、
重力加速度g=9.8
A地点の高さ =0.2メートル
B地点の高さ =0.132メートル
を式(1)に代入すると
m×9.8×0.2=m×9.8×0.132+1/2mv2
1.96m=1.2936m+1/2mv2
1/2mv2=0.6664m
mv2=1.3328
v≒1.15m/s
と速度の理論値が求められる。
また、実際の実験装置で金属球を転がし、その速度を赤外線センサーで測定すると0.93m/sとなった。
②その後BからGまでは平坦なため位置エネルギーに変化が無く等速直線運動(速度B)で運動する。G地点までの時間を測定して速度との関係からレールの長さを求める。
金属球がB地点からG地点までを通過するのにかかった時間 は1.3秒なので、これにB地点の速度の実測値(0.93m/s)とG地点の速度の実測値(0.88m/s)の平均速度(0.90m/s)をかければ、BからGのレールの長さが求められる。定規使えばいいじゃんとか野暮なことを言ってはいけない。
0.9×1.3=1.17メートル
レール②
①スタート後B地点では、A地点とB地点の位置エネルギー差が運動エネルギーとなり速度Bを持つ。
②その後BからCまでは平坦なため位置エネルギーに変化が無く等速直線運動(速度B)で運動する。
③従って、C地点ではレール②の金属球はレール①の金属球と同じ時間に到着する。
④その後CからDまでは斜面運動のため、速度が加速されD地点に達する。その結果、レール②の球がレール①の球を追い越すことになる。そこで、D地点での速度Dを求める。
mghA=mghD+1/2mv2 ・・・(1)
式にD地点の高さhD=6.2㎝(=0.062m)を代入すると、速度 は
v=1.64462761742・・
≒1.64m/s
となった。
また、実測値は1.3m/sであった。
すなわち速度D>速度Bということになる。
⑤DからE地点までは速度Dで等速直線運動で移動する。このときの速度差からレール②の球がレール①の球より速く距離D-E間を移動する。
⑥その後EからFまでは斜面を上るので速度は遅くなるが、力学的エネルギーはD地点からC地点に戻るのと同じである。従って、F地点の速度はC地点の速度(速度B)となる。
レール①VSレール②
上記の結果からレール①の金属球よりレール②の金属球の方が経路の長さに関わらず速くゴールに到着することが分かった。では一体何でそういうことになるのか、向井千秋記念館に変わって考えてみる。
まずレール①とレール②はC地点から距離が異なるので、その距離を測定した。
レール①のB~Gの距離
B~G:117cm
レール②のB~Gの距離
B~C:16.5cm
C~D:22.0cm
D~E:45.0cm
E~F:27.0cm
F~G:19.5cm
B~G:計130cm
よってレール②の距離の方がレール①の距離より13cm程大きいことが分かる。
次にレール①とレール②の速度変化の様子をグラフに示した。
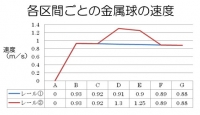
このように、レール②の速度はどの区間においてもレール①の速度と同じかそれよりも速く、レール①の速度を下回ることはないということがわかる。
問題は二つのレールの速度の差(v②-v① )が、二つのレールの距離の差(d②-d① )を補えるほど大きいかである。
レール①の平均速度の実測値は0.905 m/s
レール②の平均速度の実測値は1.09 m/s
なので、G地点に到着するタイムは
レール①が t= d①/v①
1.17/0.905=1.29281767955…≒1.29秒
レール②が t= d②/t②
1.3/1.09=1.19266055045…≒1.19秒
したがってレール②の方が速くG地点に到着することが求められた。
この結果を応用させて考えると、同じ地面に球を転がす坂の傾斜角が大きいほど、速度が速い(運動エネルギーが高い)区間が大きくなり、そのタイムも短くなると言うことになる。
※理科の先生によれば、最終的に同じ速度で走るなら、いきなりアクセル踏んで加速させちゃったほうが燃費がいいのと同じらしいが、安全性についてはわからない。
また、傾斜角を大きくした場合、レールの道のりと落差が増加し、落差に伴って速度が増加するが、道のりの増加する割合と、速度が増加する割合を比較すると以下のようになる。
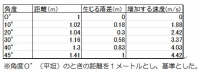
また速度の増加量は、力学的エネルギーの式に、坂の角度が変わることによって生じる落差を代入した。落差は単位円上のタンジェントと考えて求めた。
よって、どの傾斜角度でも、道のりの増加する割合よりも、速度が増加する割合の方が大きいことが分かる。
しかし、その角度があまりにも急になると、ほとんど地面に自由落下することになり、球は弾んでしまい運動の振る舞いが変わってしまう。
また、坂から地面に切り替わる部分が直線的に折れ曲がっていると運動エネルギーが地面との衝突で失われてしまうので、切り替わり部分をなめらかな曲線にすると運動エネルギーのロスはなくなる(ジェットコースターのサイクロイド曲線の話)。
ゴール地点Gの速度
力学的エネルギーが保存されるとすればゴール地点Gでの両者の速度は同じはずである。それが同じ速度であることを確かめるには、どのような実験を行ったらいいか、いくつか考えてみました。
その1
ゴール地点Gに赤外線センサーを用いた速度測定器を置いて、レール①、レール②それぞれの金属球のG地点での速度を計測する。もっとも手っ取り早い方法である。
実測値はどちらも0.88 m/sであった。さすが精密機器!
その2
ゴール地点Gにおけるレール①とレール②の高さを比べ、それが等しいかを調べる。二つのレールの高さが等しいならば位置エネルギーと運動エネルギーの割合も等しいということなので、速度は計算上等しくなるはずである。
その3
G地点付近の平坦な区間のレールの長さと、その区間を金属球が横切る時間をレール①とレール②でそれぞれ計り、金属球の速さを求め比較する。
その4
レール①とレール②に用いる金属球の質量を統一した上で、ゴール地点にそれぞれ同じ質量の障害物を置く。(障害物はレールを滑るような物にする)
この障害物に、各レールを転がった金属球をぶつけ、障害物が動いた距離を測り、レール①とレール②の運動エネルギーを比較する。
仮に二つの金属球の速度が等しいならば、その運動エネルギーも等しく、障害物が動く距離は一致するはずである。
力学的エネルギー保存の法則は、摩擦や空気抵抗を無視できるならばコースの形状の影響を受けないので、どのような経路を経ても、最終的にレール①とレール②の終点G地点の高さが等しいならば、金属球は等しい運動エネルギーを持つ。
したがって、レール①もレール②もG地点は同じ高さなので、赤外線センサーを用いた速度計測器が示した金属球の速度はどちらも0.88 m/sになったと考えられる。
スロープの傾斜と速度の関係
スロープの角度(=位置エネルギー)を4段階に設定できる実験装置を使って、それぞれの位置エネルギーがすべて運動エネルギーに変わったとして力学的エネルギーの保存の法則を用いて金属球の速度を計算で求める(理論値)。また、赤外線センサーを用いた速度測定器を用いて金属球の速度を実測する。
計算で求めた速度(理論値)と実測値とを表にまとめ比較検討した。
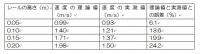
まず、レールの高さが上がり、斜面の傾斜角度が大きくなると、速度は理論値も実測値も増加することが分かる。しかし、その増加する割合は理論値よりも実測値の方が小さい。
理論値よりも実測値の速度の方が遅い理由としては、摩擦力と空気抵抗が考えられるが、理論値と実測値の誤差を調べると、その誤差はレールの高さが高いほど大きいことが分かる。
仮に速度の実測値を理論値よりも下げている原因が摩擦力だった場合、傾斜角が急なほど大きく摩擦がかかっていることになるが、このとき運動を妨げる力である動摩擦力fは動摩擦係数μと垂直抗力Nの積となるため、金属球にかかる垂直抗力がレールの高さが高くなるにしたがい低下する以上、これは考えられない。
次に空気抵抗であるが、空気抵抗は物体の速度がある程度大きい場合は、速度の二乗に比例して大きくなることが知られている。つまり速度が2倍になると空気抵抗は4倍に、速度が3倍になると空気抵抗は9倍になる。
上の表のレールの高さ0.05mと0.10mの結果を比較すると、速度の理論値は1.41倍に、誤差は2.22倍となっている。また、0.05mと0.15mの結果を比較すると速度の理論値は1.72倍、誤差は3.26倍となり、誤差が速度の理論値の二乗分だけ生じていることがわかる。したがって理論値と実測値との誤差の原因は空気抵抗であると考えられる・・・と私は願いたい。