この標本誤差は、母集団と標本のデータ数が近づけば近づくほど小さくなる(全数調査では標本誤差は発生しないから)。これを大数の法則という。
正規分布
別名ガウス分布。パラメータ(後述)を説明する際には、ノーマル・ディストリビューションの頭文字Nを用いる。
身長や体重、偏差値など、最も数が多い平均的(フツー)な集団が山の頂上を形成し、フツーじゃない奴はその程度に応じてどんどん山の裾野に追いやられていくという分布。
グラフの形自体はシンメトリーでシンプルだが、式にすると恐ろしいことになる。ちなみにμ(ミュー)は平均、σ2(シグマ)は分散を表す。
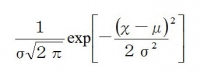
exp[ほにゃらら・・・]は経験値・・・ではなく、エクスポネンシャル・ファンクション(指数関数)の略で、対数関数を微分するための無理数(ネイピア数e≒2.71)の指数を表している。
ちなみにネイピア数は超便利で、1を何乗しても1であるように、e^xを何回微分しても答えがe^xのまま変わらない。
そもそも正規分布のグラフは、もっとも簡単に表すと
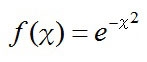
であり(急激に減少するタイプの関数)、指数にも指数がついちゃっているので、ややこしいから
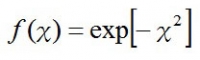
と、表し直す。
次に正規分布は、デジタルではなく、身長のようにスペクトラムなデータを扱うので、その合計値は∑ではなく∫(インテグラル)を使用する。つまり積分(グラフの内側の面積を、シュレッダー的に無限に細かく千切りをしてから、再び貼り合わせて求めること)をする。
ちなみにインテグラルは、足し算の答えのSUMの頭文字のSを縦にビヨーンと引き伸ばしたもので、シグマとあんま意味は変わらない。
ただシグマは1番からn番までを足していたが、インテグラルは数直線の原点0の左右に広がる正の世界と負の世界のそれぞれの地平線の向こう側まで足してしまう。
オレ達と一緒に行こうぜ!無限大の彼方へ!(懐かしい)
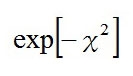
を積分すると、ガウス積分の公式より、その値は円周率の平方根と等しくなるので
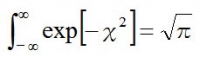
また、正規分布はそこに含まれるすべての集団の割合の合計値が1(=100%)になるので、方程式の右辺を1にするために、両辺を√πで割る。
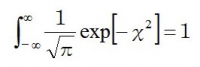
個人的にはこの形で終了でもいいと思うんだけど、この式を微分すると、係数で×2が出てきちゃうので、その手間を省くためにXを変数変換(※)して調整する。
※X→√2×X’と変換する(√2で割る)と指数は複雑になるが、微分したあとの係数が1になる。
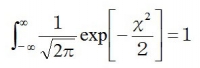
こうしてできた式が、平均が0(正規分布のグラフの真ん中を示す軸zがX=0、つまり中心にある)、分散が1(標準偏差も1)という、最もわかりやすい正規分布、標準正規分布の式である。
実際は平均が中心からずれてたり(軸zがプラスにズレたりマイナスにズレたり)、分散も1より小さかったり(グラフの幅が狭まる)、1よりも大きかったり(グラフの幅が広がる)するので
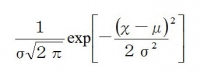
として、μとσに具体的な値を代入し、グラフの形を求める。
母数(パラメータ)
母集団分布の状況を曲線で示したときに現れる、そのモデルを特徴付ける特性値のこと。
たとえば、正規分布の曲線の場合、平均μと分散σ2のふたつの母数の値が決まれば、曲線の形状が決まることが、さっきの式で理解できる。
標本の抽出方法
いろいろあります。
無作為抽出
母集団から完全にランダムに標本を選ぶというイメージがあるが、厳密には母集団が含む調査対象をすべて同じ確率で選ぶ抽出方法を指す。そう言う意味で乱数は完全なカオスってわけでもない。
単純無作為抽出法
母集団のすべてのデータをナンバリングして標本を選ぶ方法。母集団の大きさがそれほどでもない時に使える。
系統抽出法
母集団のすべてのデータをナンバリングし、最初に一つサンプルを選び、このサンプルのナンバーから一定間隔で次の標本を選んでいく方法。
多段抽出法
都道府県を選ぶ→選ばれた都道府県の中の市町村を選ぶ→選ばれた市町村の中の地区を選ぶ・・・といったように段階的に集団を選ぶ方法。
層別抽出法
母集団に含まれる各グループの構成比率を考慮して標本を選ぶ抽出方法。
例えば母集団の構成が、Aグループ70%、Bグループ30%で、ここから100人のサンプルを選ぶ場合、Aから70人、Bから30人を選ぶとあらかじめ設定してしまう。
最尤法
現在手元にあるサンプルは最も手に入れやすい、一番妥当なサンプルであると仮定する方法。例えばコイントスを10回して、表が6回、裏が4回出たとすると、このコインで表が出る確率は60%が妥当だと考える。
とはいえ、このコインが表を出す本当の確率はよくわからないので、これをpとすると、裏が出る確率は(1-p)となり、先ほどの試行結果が出る確率(尤度関数L)は
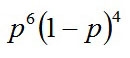
となる。では、この式の確率を最大にするためのpの値はいくつなのかを考えると、上の式の尤度関数か対数尤度関数の答えを最大化させればいいので、比較的計算が易しいほうの対数尤度関数で計算すると
これを微分して答えが0になれば、正規分布に傾き0の接線が引け、それが可能なポイントはグラフの頂点だけだということで、尤度関数の確率は最大になる。
ということで、微分してみると
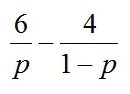
分数の足し算なので、通分して
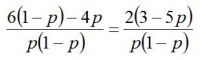
よってこの答えを最大化するにはpに3/5を代入すれば分子の()の中が0になり、答えが0になるので、p=3/5、すなわち6/10で、やっぱり60%となる。
最尤推定量
この話を一般化すると、パラメータθの母集団f(x;θ)からn個の無作為標本をゲットした場合、尤度関数L(θ|x1,x2…xn)は
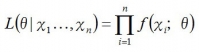
また、対数尤度関数は
これを最大化させるパラメータは最尤推定量(θハット)と呼ばれる。
例えば、平均μ、分散σ2の正規分布N(μ,σ2)からn個の無作為標本x1,x2,・・・,xnをゲットしたとして、この時の母集団の平均μの最尤推定量と、分散σ2の最尤推定量を求める。
まず、下ごしらえ。
n個の無作為標本が平均μ、分散σ2の正規分布に従う確率は、1個目~n個目までのデータをかけていくので、小学館の机を使って
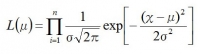
これを計算すると
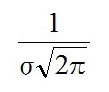
の部分は普通にn回かければよく、
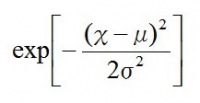
の部分は指数なので、指数法則(※)より、指数同士をn回足せばいいので

かなり複雑なので、対数尤度関数の形にして
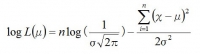
指数をマイナスにすると分母が累乗されるので
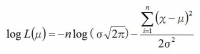
この式を最大にするμの値を求めればいいので、この式を微分するわけだが、この式にはμとσの二つのパラメータがあるので、まずは平均μについてだけ微分する。つまり、σを定数としてμで微分する。
こういう複数のパラメータがある際、任意のパラメータだけを微分することを偏微分といい、偏微分をしたよという意味の∂(デルもしくはデルタ、ディー)をつける。
指数のない
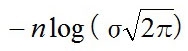
の部分は消え、
指数2のある
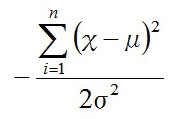
は指数の2が消えて、係数の2がつくので
この値が0になればよいので
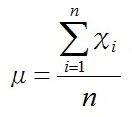
の時に分子が0になり、対数尤度関数は最大になる。
よって、平均μの最大推定量μ^(ミューハット)は
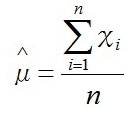
で、標本平均値と同じということがわかる。
次に、分散σ2の最尤推定量を求める。今度はσ2で偏微分すればいいので、まずは微分しやすいように式の形を変える。
log()の平方根は、2で割ると()の中が2乗されて消えるので
分配法則を使って
ここでσ2で偏微分して(※y=logxの微分はy′=1/x)
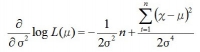
この分数の引き算を通分して
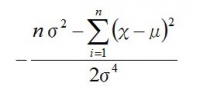
この式が=0になればいいので
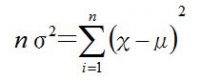
よって、分散σ2の最尤推定量σ2^は
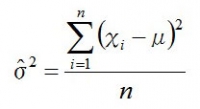
統計的仮説検定
生まれたばかりのラット15匹のうち、8匹には飼料Aを、7匹には飼料Bを与え飼育した。一定期間後に体重(g)を量ったところ以下のようなデータが出た。
飼料A 46.9 46.2 47.1 45.0 48.7 47.6 46.8 48.6
飼料B 48.6 49.2 47.5 51.0 50.3 49.0 49.7
このデータから餌の違いがラットの生育に影響を与えているかどうかを、有意水準(危険率)5%で仮説検証する。
ただし、ラットの集団は正規分布に従い、飼料Aの群れと飼料Bの群れの分散は等しいとする。
二つのグループがある場合の分散は
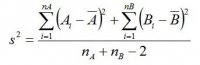
つまりグループAのそれぞれのラットの体重とグループAのラットの平均体重の差の合計を二乗した値と、グループBのそれぞれのラットの体重とグループBのラットの平均体重の差の合計を二乗した値を足し、さらにラット15匹-2=13で割る。
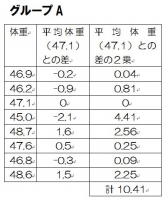
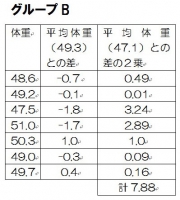
したがって、分散は
この推定量を使って
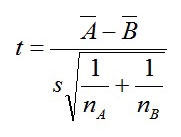
が自由度13のt分布の95%のエリア内かどうかを確かめる。
Sはだいたい1.19なので
となる。
最後に、この-3.55が自由度13のt分布の95%のエリアに入っているかを、テキスト巻末資料のt分布の棄却点の表で確認する。
すると自由度13のt分布の棄却点は±2.160なので、-3.55は自由度13のt分布の95%のエリアから外れていることがわかる。
つまり「餌の違いがラットの生育に影響を与えている」という仮説が実際に正しい場合、上記のデータが現れる確率は5%以下であるため、この仮説は有意水準5%で棄却される。