ここで自分の英語アレルギーが足を引っ張るとは思わなんだ。
この分野に関しては、地道にコツをつかんでいかないと、式の意味すら分からないということが判明したため、急遽、統計学に関する本を4冊ほど追加注文。ごちゃごちゃした数式とにらめっこしながら、元気にネットカフェで頑張ってます。
ちなみに今日から生物学実験が始まったんだけど、生物学の教授、超いい人。話超面白い。
ただ、その優しさに騙されてはいけない!理科の単位で最もカラい評価なのが、イエッス、生物学なのだ!試験範囲が生物学全て(細胞、植物、動物、発生、遺伝、生理、分類、生態、環境、進化・・・)という前代未聞の広さで、北欧の生物学のテキストを暗記しなければならず、しかも、テキストに書いてあることをテストでそのまま書いても合格しないという恐ろしさよ。
まあ自分は生物学が好きだから、割ととんとん拍子にとれたんだけど、苦戦した人が多かったようで、一体どんなバケモンがバイオを担当してたんだと思ってたら、超いい人。この優しさの仮面の裏は般若だね。(C)まる子
参考文献:塚田真一著『Primary大学テキストこれだけはおさえたい確率統計』、吉田寿夫著『本当にわかりやすいすごく大切なことが書いてあるごく初歩の統計の本』、今野紀雄著『図解雑学統計』、馬場敬之著『スバラシク実力がつくと評判の統計学キャンパス・ゼミ―大学の数学がこんなに分かる!単位なんて楽に取れる!』
統計
統計学の歴史は古く、古代文明のセンサスまでさかのぼるらしい。統計の語源は国家と一緒でステータスで、国家を運営するためには国民の統計が欠かせないというわけである。
近代的な国際関係ができた17世紀のウェストファリア条約以降は、国家の運営だけではなく、疫病の流行や、天文学、生物学といった自然科学にも応用され(あと優生学)、その後、各学問における統計学的な規則性は、そっくりそのまま他の分野に流用できる普遍性を持つことがわかってきた。
ここらへんから素人お断りな抽象的な数理モデルが幅を利かせるようになり、現在ではエクセルで決まったコマンドを打ち込むとコンピュータが勝手に計算してくれるまでになった。
全数調査(記述統計学)
イギリスの統計学者ピアソンが大成。調査対象を全部しらみつぶしに調べるタイプ。
データが膨大でそこから傾向を導き出すのは非常に難しい。よって、平均をとったり、棒グラフや円グラフにしてわかりやすく視覚化するなどの工夫が必要になる。今回の統計学覚え書き①はその手法についてまとめます。
標本調査(推測統計学)
調査対象の一部しか調べないタイプ。1925年に経済学者のフィッシャーが考案。
世論調査や視聴率のように調査対象の集団が大きすぎる場合や、製品の品質管理における破壊検査など、とてもじゃないけど調査対象をすべて調べられない場合におこなうサンプル調査。全体(母集団)の一部である部分(標本)から、全体を推測するという考え方。
ベイズ統計学
1950年代に誕生。母集団を前提にしないで、現時点における情報だけで計算してしまう、かなり主観的なタイプ。
有名なのは、クイズ番組のモンティホール問題というやつで、これはいまだに決着がついていない。計算の仕方でどうにでもなるらしい。
データ
いろいろあります。
質的データ(カテゴリカルデータ)
割合は求められるが、平均は求められない、もしくは求めても意味がないデータのこと。
さらに、質的データは、性別や血液型といった順序関係がないデータである名義尺度と、現在の内閣は「非常に満足」「やや満足」「どちらでもない」「やや不満」「不満」など順序がつけられるデータである順序尺度に分けられる。
量的データ
数値によって記録できるデータ。
身長・体重といった連続的(アナログ)な値をとる連続型データと、さいころの目といった非連続的(デジタル)なとびとびの値をとる離散型データに分けられる。
比尺度のデータ
0の意味が絶対的な意味を持つデータのこと。身長など。0cmは長さがない。
間隔尺度のデータ
0の意味が相対的な意味を持つデータのこと。気温など。0℃は温度がないわけじゃない。
次元
観測値の項目のこと。項目がひとつだけなら一次元データ、ふたつなら二次元データ。三次元以上は多次元データと呼ばれる。次元が複数のデータを分析する場合は多変量統計解析を行う。
グラフ
いろいろあります。
棒グラフ
各自動車会社の販売台数といった、ランキングを表示するときわかりやすい。
折れ線グラフ
時間とともに変化する歴史的なデータをとらえるときわかりやすい。
円グラフ
それぞれのデータの構成比率がわかりやすい。
ヒストグラム(柱状グラフ)
縦軸を各階級の度数、横軸を階級にしたグラフで、データの分布状況がわかりやすい。
箱ひげ図
名前が危機一髪的で面白い。各データの最小値と最大値のギャップをひげの長さで、データのばらつきを表す第1四分位点(小さい順から1/4番目のデータ)と、第3四分位点(小さい順から3/4番目のデータ)のギャップを箱の長さで表すグラフ。ちなみに箱の間には中央値(小さい順にデータを並べたときちょうど真ん中のデータ)の線が入る。
相関図(散布図)
縦軸に湿度、横軸に最高気温といったように、相関性のありそうなデータを両軸に取った図のこと。
3つの相関性のあるデータを一度に図にしたい場合はバブルチャートになる。ロープレの各ステータス(HP、MP、攻撃力、防御力、素早さ)のような、それ以上の種類のあるデータをまとめるときはレーダーチャートを使う。
縮約値
データの特徴を表してくれる値。いくつかは脱ゆとりで中学校の数学で習うことになった。
モード(最頻値)
質的データの場合に、観測される頻度が最も多いカテゴリーをいう。たとえば都知事選の出口調査における百合子みたいな。
これはデータの分布をグラフ化したときに山(ピーク)が一つだけのときに有効な値となる。
メジアン(中央値)
データを大きさ順に並べたとき、ちょうど真ん中にくるデータの値。ゴレンジャーをイメージすればわかるように、データの数が奇数の場合は真ん中のメジアンは決めやすいが、偶数の場合は真ん中がどっちか決められないので、二つの値を合計して二で割っちゃう。
メジアンは、例えばGDPが超高い国があったとして、じゃあ国民全員が金持ちなのかな、いや、実はごく一部の超ウルトラ金持ちが平均を引き上げてるんじゃないか?みたいな疑問を持ったときに便利です。
平均
最も有名な縮約値。
たとえば30人のクラスのテストの平均点は、生徒30人分の点数を一回すべて足して(集めて)、その値を30で割れば出せる。つまり、n個のデータをすべて足して、その数をnで割ると出せる。まさに社会主義の富の再分配。
xの平均はxの上に横棒を載せてxバーとするのだが、案の定タイプできないので、x均とします。
Xの平均=(1番目からn番目までの全部のデータの合計)/n
x均=(x1+x2+x3+・・・+xn)/n
シグマを使って表すと、小学生でも理解できる計算が一気に遠い存在になる。
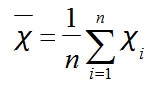
この時の∑は「xに関するデータを1番目からn番目まですべて足す」という意味。
これをnで割るので、×1/nをしている。
ちなみに1番目からn番目までかける場合は、シグマではなくパイの大文字のΠを使います。こいつずっと読み方わからなかった。小学館の机だと思ってた。
ちなみに、元のデータの単位を変えてxiがaxi+bになったとき、再びその平均を出す場合は、元データの平均にaをかけて、定数bを足す。
なんでそうなるかの計算は難しくはないんだけど、Σの計算式をタイプするのが非常に面倒くさいので、ワードの最新版を買ったら打ち込みます。
度数
それぞれの階級に該当するデータの数のこと。例えば点数が52点だった生徒は「2人」など。
級代表値
階級に「61~70点」などと幅があった場合、その階級を代表する値。ここでは真ん中の「65点」がそれ。
相対度数
各度数が度数の合計に占める割合。
各級代表値×各相対度数を全度数分Σですべて足すと、平均値が出る。
トリム平均
データの特異値(変に大きすぎたり、小さすぎたりする観測値)の影響をカットするため、データの上位と下位のいくらかを除いて、残ったデータの平均をとる方法。
吹奏楽コンクールやフィギュアスケートなど、複数の審査員がいる競技でよく用いられる。金属の熱伝導率の測定実験で用いた平均の出し方。
ミッドヒンジ
第1四分位点と、第3四分位点の平均。第1四分位点と、第3四分位点の値を足して、2で割る。
平均偏差
それぞれのデータと、平均値との差(Xi-X均)を、平均化するとする。
すると、当たり前っちゃ当たり前だけど、この値を全度数分、シグマを使って足すと(あとnで割るんだけど)、平均値に届かないデータ(負の数)も、オーバーするデータ(正の数)も互いに綺麗に相殺され、値は0/nとなり、答えは常に0になる。
これだとデータの偏りが何もわからないため、(Xi-X均)を|Xi-X均|と絶対値にして、平均化したものを平均偏差という。
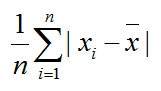
分散
平均偏差では(Xi-X均)を絶対値にしてΣですべて足したが、(Xi-X均)を2乗したものは分散と呼ばれ、S2で表される。
なぜに2乗かというと、平均偏差の時にも言ったように(Xi-X均)で計算をすると、正の数と負の数が出てしまうので、2乗することで符号をプラスに統一しているというわけ。じゃあ4乗でも6乗でもいいじゃんって感じなんだけど、まあ確かに符号はプラスになるんだけど、何乗もしちゃうとデータの誤差もそれだけ指数関数的に増大しちゃうので、偶数で一番小さい2が選ばれている。
ちなみにxiの単位を変換し、xiが(axi+b)となっても、分散は元の分散の値にaの2乗をかけた値になるだけで、定数bは関係しないことが分かる。
標準偏差
平均偏差はそれぞれのデータと平均との距離(絶対値)の平均なので、もとのデータと単位がそろっているが、分散の場合は(Xi-X均)を2乗しているので元のデータの単位がそのまま使えない。そのため一般的にデータのばらつきを表す場合は、分散の平方根を求める。これを標準偏差といいSで表す。
正規分布の山なりのグラフは、標準偏差が小さいほど、グラフの幅が狭く山の高さが高くなり、標準偏差が大きいほど、グラフの幅が大きくなり山の高さは低くなる。
変動係数
身長や体重といった個体差のばらつきの程度を調べる際に求める係数(%)。
標準偏差を平均で割って100をかける。
歪度
分布の山の頂上が左右のどこにあるか、つまり山のシンメトリー具合を表す。
歪度がプラスだと頂上は中心よりも左に、歪度が0だと左右対称(正規分布)、歪度がマイナスだと頂上は中心よりも右になる。
尖度
分布の山の尖り具合を表す。尖度がプラスだと尖り頂上は高くなり、尖度が0だと正規分布、尖度がマイナスだと山はなだらかに低くなる。
相関
xとyの2つのデータが影響しあっていること。
例えば土地の面積(x)と家賃(y)など。
xy座標の(x均,y均)に接近するほど相関性は強い(右肩上がりの角度45°の直線になる)。
最小二乗法
2つのデータを相関性を示す直線を回帰直線というが、その直線を求める際に用いる一つの手段。マリ・ルジャンドルが考案。
仮に回帰直線をy=ax+bとしたとき、その傾きと切片を求める場合、各データのポイント(xi,yi)を考えると、一次関数の左辺はyiで右辺はaxi+bとなり、左辺と右辺にはズレが生じる。
このズレyi-(axi+b)を二乗した値を度数分すべて足した値が最小になるような定数aとbを求める方法を最小二乗法という。
これを、またしちめんどうな計算をして求めると
a=Sxy/Sxx
b=y均-ax均
となるので、これをy=ax+bに代入すると回帰直線の式は
y=(Sxy/Sxx)x+{y均-(Sxy/Sxx)x均}
y=(Sxy/Sxx)(x-x均)+y均
ちなみにSxyは共分散、bは回帰係数と呼ばれる。