しかし、数学を解いていると時間があっという間に過ぎてタイムワープするよね。そして寝不足。そりゃ、円周率やフェルマーの最終定理の証明に人生すべてを使っちゃう人も出てくるよね。
この前買った統計学の本にも「なんと!このテキストは通し読みがたったの二週間でできます!」みたいに書いてあって、軽く衝撃を受けたもんw読書に対するイメージが文系のそれとは全く異なるわけだ。
だから高校の数学のカリキュラムがいかに無茶な詰め込みをやっているのがよくわかるよね。初見は理解に時間がかかるのは当たり前なのに、自分の学校なんかは理系進学校とかで3年分を2年で終わしちゃってたしね。当然取り残されたしたよ、あたしゃ(C)浅香光代さん
むしろ、あれでついていける方がおかしいんだよな。エリート以外をそぎ落とすためのカリキュラムなんだろうな。
参考文献:塚田真一著『Primary大学テキストこれだけはおさえたい確率統計』
確率の基本用語
中学~高校で習う言葉をおさらい。
おう、なつだぜ。おれはげんきだぜ。カップとキャップがややこしいぜ。
施行
結果が偶然に支配されている実験のこと。ある施行(サイコロを転がす)を行った時に、起こり得る結果(2や5)を根本事象、これを集めた集合を標本空間Ω(1、2、3、4、5、6)という。
数学的確率(ラプラスの確率定義)
有名なラプラスによる定義(Since1812)。ある施行(例:サイコロをふる)についての標本空間のサイズがn(1~6の目=6通り)で、どの根本事象(目)も、“同様に確からしく”起きるとき、Eが起きる場合の数をrとすると、Eが起きる確率P(E)は
P(E)=r/n
経験的確率(統計的確率)
明日の天気や保険会社の掛け金など、手持ちの統計(データ)をもとに未来を予測する確率。
サイコロを振る回数をどんどん増やしていけばいくほど、ある目が出る回数はだんだん1/6に近づいていくという考え方。
つまり試行回数をn、そのうちEが起きた回数をrとすると
P(E)=lim(n→∞)r/n
リヒャルト・フォン・ミーゼスが定義(Since1928)。ちなみに兄のルートヴィヒ・ミーゼスはハイエクの師匠として有名なオーストリア学派の経済学者。
全事象
必ず起こる事象。
空事象
絶対起こらない事象。
和事象
AかBのどっちか一方が起きる事象のこと。A∪B(AカップB)と表す。
AorBのがわかりやすい気がする。
積事象
AtoBが同時に起きる事象のこと。A∩B(AキャップB)と表す。
AandBのがわかりやすい気がする。
A∩Bが空事象であるときは、AtoBは互いに排反であると呼ばれる。
余事象
Aが起こらない事象。Acと表す。Aは起こるが、Bは起こらない事象はA∩Bcとする。
ド・モルガンの法則
モーガンではなく、あえてモルガンと読む。ベン図を書くと分かりやすい。
①Aが不可能またはBが不可能である場合、AとBを兼ねることは不可能。
Ac∪Bc=(A∩B)c
②AとBが同時に不可能である(AもBも起きない)場合、AまたはBであることは不可能。
Ac∩Bc=(A∪B)c
確率分布
ひとつのサイコロを2回投げた時、出た目の大きい値をxとする。
このときxの確率分布および、その平均と分散を求めよ。
x=1の時
2回とも1の目の時だけなので
1/6×1/6=1/36
x=2の時
①1回目が1、2回目が2の時
②1回目が2、2回目が1の時
③1回目も2回目も2が出た時
の3パターンあるので
3/36
もしくは(1回目も2回目も2以下の目の時)-(x=1の時)なので
2/6×2/6-1/36=3/36
x=3の時
同様に(1回目も2回目も3以下の目の時)-(1回目も2回目も2以下の目の時)なので
3/6×3/6-4/36=5/36
x=4の時
(1回目も2回目も4以下の目の時)-(1回目も2回目も3以下の目の時)なので
4/6×4/6-9/36=7/36
x=5の時
以下省略
5/6×5/6-16/36=9/36
x=6の時
6/36×6/36-25/36=11/36
したがって確率分布の平均は
(1×1/36)+(2×3/36)+(3×5/36)+(4×7/36)+(5×9/36)+(6×11/36)=161/36≒4.472
分散は、(各事象と平均との差の二乗)×その事象の確率なので
{1-(161/36)}^2×1/36
+{2-(161/36)}^2×3/36
+{3-(161/36)}^2×5/36
+{4-(161/36)}^2×7/36
+{5-(161/36)}^2×9/36
+{6-(161/36)}^2×11/36
となり、通分して分子を足したり、電卓を使って二乗すると
15625×1/46656
+7921×3/46656
+2809×5/46656
+289×7/46656
+361×9/46656
+3025×11/46656
15625/46656
+23763/46656
+14045/46656
+2023/46656
+3249/46656
+33275/46656
=91980/46656
≒1.97
倍数の判定方法
それぞれ1、2、3、4が書かれたカード4枚を無作為に並び替えて4ケタの数字を作る。
この時出来た数字が4の倍数である確率を求めよ。
無作為に並べて出来る4ケタの数は4×3×2×1=24通り。
4の倍数は100の位より大きい位はすべて4で割れてしまうので、下2ケタだけ確認すればいい。
4(250×A+25×C)+10×C+1×D
4ケタの数字の下2ケタが4の倍数になる場合は、12、24、32の3通りなので、4の倍数になる確率は3/24=1/8
ベイズの定理
Aが起きる確率×Aが起きて更にBが起きる確率と
Bが起きる確率×Bが起きて更にAが起きる確率は
AとBが同時に起きる確率と等しいという定理。
P(A)×P(B|A)=P(B)×P(A|B)=P(A∩B)
Aを「ハンバーガーを注文した客の数」、Bを「ポテトを注文した客の数」などにして、ベン図を書いて実際に計算してみるとわかりやすい。
例えば100人のお客がサンドサンドバーガーコスモ店にやってきて、そのうちハンバーガーをオーダーした客が70人、ポテトをオーダーした客が30人いたとする。
さらにハンバーガーとポテトをどちらもオーダーした人は100人中20人いた。
ハンバーガーとポテトをどちらも注文した人の確率は言うまでもなく2/10
ハンバーガーを注文し、さらにポテトを注文した人の確率は70/100×20/70=2/10
ポテトを注文し、さらにハンバーガーを注文した人の確率は30/100×20/30=2/10
よってどれも同じ確率である。
もう一つ大学で出された問題をやってみる。
同じ形をした3個の箱A,B,Cがある。
箱Aの中には赤玉1個と青玉1個が入っている。
箱Bの中には赤玉1個と青玉3個、箱Cの中には赤玉2個と青玉3個が入っている。
3つの箱の中から1つの箱を選び、選んだその箱から玉を1個無作為に取り出すとき、次の確率を求めよ。
(1)取り出した玉が青玉である確率
青玉が出る事象をbとすると、その確率P(b)は
P(b)=P(b∩A)∪(b∩B)∪(b∩C)
=P(b∩A)+P(b∩B)+P(b∩C)
箱Aを選んで青玉を取り出す確率P(b∩A)は
1/3×1/2=1/6
箱Bを選んで青玉を取り出す確率P(b∩B)は
1/3×3/4=1/4
箱Cを選んで青玉を取り出す確率P(b∩C)は
1/3×3/5=1/5
したがって
取り出した玉が青玉である確率は
1/6+1/4+1/5=37/60
(2)取り出した玉が青玉であるとき、箱Aが選ばれた確率
箱Aを選んで青玉を取り出す確率/取り出した玉が青玉である確率
なので
1/6/37/60 =10/37
確率密度関数
根本事象がデジタルな離散形の確率ならともかく、連続型の確率の場合、その事象がピッタリ起きる確率はほとんどゼロであるため、確率を求めたい事象にA以上B以下といった具合に幅を持たせる。
この考えのもと、連続型確率変数 X(どの根本事象が起きるかによって変わる変数。サイコロの目なら1~6のどれか) に対して,Xが a 以上 b 以下となる確率が
P(a≦X≦b)=∫[a→b]f(x)dx
である場合、f(x)は確率密度関数と呼ばれる。
また、このときの平均は、確率変数X×確率密度関数f(x)の積分となるため
E(X)=∫[a→b]Xf(x)dx
連続型確率変数Xの一次変換Y=aX+b (aとbは定数)の平均は
E[Y]=a E[X] +bになることを確かめてみる。
確率密度関数をf(x)、確率変数をXとする
E(X)=∫[-∞→∞]Xf(x)dx
Y=aX+bとして
E(Y)=∫[-∞→∞] Yf(y)dy
=∫[-∞→∞] (aX+b)f(x)dx
=a∫[-∞→∞]Xf(x)dx+b∫[-∞→∞]f(x)dx
=aE[X]+b※
※∫[-∞→∞]f(x)dxの確率は1(100%)になるため。
確率分布の平均
f(x)=k(x^2-1)(-1≦x≦1)
f(x)=0(x<-1、1<x)
が確率密度になるようにkの値を求め、その確率分布の平均を求めよ。

上の式を積分すると
1の積分はx
x^2の積分はx^3/3なので
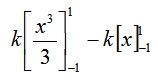
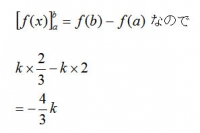
-4/3k=1なので、k=-3/4
確率分布の平均は
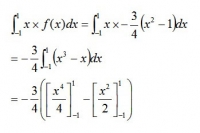
※カッコの中が1/4-1/4と1/2-1/2になるので
平均は0である。
モーメント(積率)
次の日頑張ったので追加。モーメントとは確率分布の特徴を表す量。
E[X]を確率の期待値(平均値)、次数をkとすると
離散形では
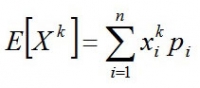
連続型では
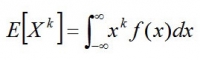
となり、1次(k=1)だと期待値(平均値)、2次(k=2)だと分散、3次(k=3)だと歪度、4次(k=4)だと尖度が求められる。
モーメント母関数
微分して任意の実数tに0を代入すれば、1次、2次、3次・・・と、すべての次数のモーメントが得られる関数をモーメント母関数(モーメント・ジェネレーティング・ファンクション)という。
離散形では
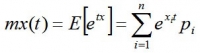
連続型では
モーメント母関数は微分が無制限にできるので、テーラー展開(Xのべき乗の多項式に展開すること)ができる。
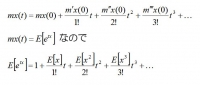
標準正規分布のモーメント母関数
平均=0、分散=1の標準正規分布の式は
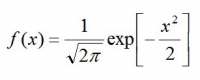
なので、連続型の方の式に代入すると
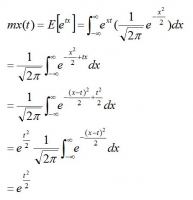
※正規分布の式を-∞~∞の区間で積分すると1になる(確率関数なので)。
よって標準正規分布のモーメント母関数は
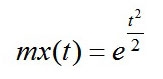
となる。
このモーメント母関数を1~4階微分して導関数を求めると、それぞれ
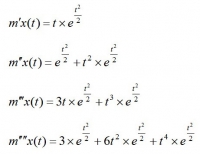
となる。(※)
これらの式に、それぞれt=0を代入すると
1次モーメントは0
2次モーメントはeの0乗の答えは1になるので1
3次モーメントは0
4次モーメントは一番左の項だけ生き残って3×1=3
となる。
(※)こしさんの解説(ありがとうございました!)