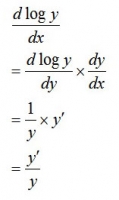実際ゼノンも直線の無限分割を批判する文脈で、このパラドックスを論じたらしい。シュレーディンガーのネコ的に。
こういう脳が疲れた時にこそ『ペット』のようなバカ映画よ。あと、この前いまさらだけど『バトルロワイヤル』観た。なんも内容がなかった。公開当時は、すごいセンセーショナルな内容で、これ以後サブカルで「殺し合いゲームもの」みたいなジャンルができたような気もするけど、私はなんといっても酒鬼薔薇世代だからな。こういう「最近の中学生はモンスター」的な映画に、すごい嫌悪感があった（『告白』とか）。
そもそも子どもっていうのは「おとな」と「こども」のように二元的に隔てられうる種族じゃないわけで、時間的な経過点なわけじゃん。来た道、行く道で。
まあそういうマスコミの短絡的な報道を、この映画は皮肉ったのかもしれないんだけど、鑑賞してみてびっくり。全くテーマや内容がないww
ただ中学生がサバイバルゲームやって撃ち合うだけ。超テレビゲーム。たけしさんが出てくるんだけど『アウトレイジ』のような痛さはゼロ。
例えば、マリオでクリボーを踏み殺すとき、そんな罪悪感ってないじゃん。この映画も何十発もマシンガンの弾があたっているのにみんな結構平気なんだよ(^_^;)この映画のマシンガンって、かめはめ波みたいなもんで様式美なんだよな。でもサブカルチャーって本来はそんなものなのかもな。
逆に、ここまで暴力をリアリティのないものとして描けるんだってことにゾッとしたっていうのはある。だから国会がやばいぞって動いたんだろう。そう言う意味で女の子が戦車乗るやつと変わらねえんだ。弾が当たったら死ぬか死なないかの違い。
で、キャラが死んでも、クリボーが死ぬレベル。ゲームやってるとそういう感情が麻痺するのかもしれない。そういや、自分の時代ってテレビゲームをやる女子って少数派だったからさ、たまにいたよね。あまりテレビゲームやらない女の子がクリボー踏む時に「ごめんなさい！」って言ったり。あのピュアな感性を忘れずにいたいものよ。
そんなわけで、映画観るのに頭使いたくないっていう客が多いのも、今ならわかるわ。学生は学校以外で頭を使いたくないのだ。
逆関数
y＝２Xは、YはXを二倍した値という意味だが、これをXの視点から考えると、XはYを二で割った値ということになる。
この時のX＝Y／２を逆関数という。
三角関数の逆関数
三角関数では、Y＝tanXを満たすXは複数あり、ひとつに絞られないため
X＝arctanYみたいに表す。
これを踏まえて
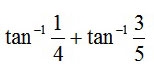という逆三角関数の足し算の値を求める。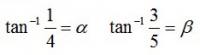
はタンジェント（正接）の逆関数（アークタンジェントarctan）であるので
とすると
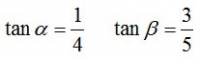
なので
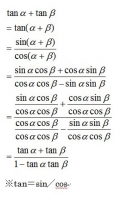
※tan＝sin／cos
上のタンジェントの加法定理の式に代入すると
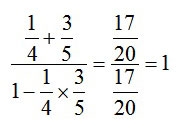
タンジェントが１になる角度は45°（＝π／４）なので
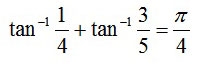
逆三角関数の微分
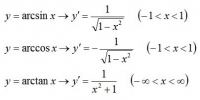
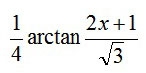
を微分すると
２／√３有理化をして
極座標
ある点P（x，y）が座標上にあったとき、点Pの原点からの距離rと、その点と原点を結んだ直線の傾き（角度）θをまとめて表した（r，θ）を点Pの極座標という。
このとき、点Pと、原点と、点（x，０）で直角三角形を作ると
x＝r×cosθ → cosθ＝x／r
y＝r×sinθ → sinθ＝y／r
rは三平方の定理から
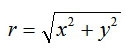と表せる。曲線
を直交座標（※）で表した時の方程式は、二倍角の公式を使って
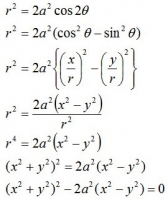
となる。
（※）座標を表す直線が直交する方眼紙のような座標。中学校で習うデカルト座標
対数微分法
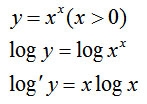
を微分すると、両辺をxで微分するので（※）
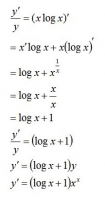
（※）yについての式である
をxで微分するにはちょっとした工夫が必要になってくる。①yをxで微分するとy'
②
をyで微分すると１／y①②より合成関数の微分と考えて
