政治学でよく取りざたされるイシューが、「政治を(プロから)市民の手に!」っていうやつなんだけど、そのテーゼが本当にどれほどのもんなのかが、世界最強の国で現実に確かめられるっていうのはかなり興味がある。
あの人本当に素人だからな。好奇心で☢ボタン押されちゃたまったもんじゃないけど、これは何もアメリカに限ったことじゃなくて、世界中でこの手のポピュリスト政治家が国を動かす地位に就いているから、そう言う意味では情報社会の当然の流れなんかなって思うよ。
有権者は難しい議論よりもプロレスの方が楽しいっていうね。もう一つがずいぶん前にブログでも書いたけど、生活という利権の問題だよね。ここを突かれると民衆っていうのはわりと力学的に動かされちゃうのかなって。ひとごとならともかく、自分の生活がかかっている苦しい立場の人が藁をもすがる思いでトランプさんを選んじゃった、選ぶ他なかったっていう、そんな流れだったんじゃないか。そういう人たちに対する想像力がエスタブリッシュメントやヒラリー陣営にはなかったのかもしれない。
まあでもトランプさん、政治家ではないけどプロの実業家(と悪役レスラー)ではあるから、アメリカという企業を立て直せれば凄いけどな。そのへんで私が好きなサンダースさんよりも実行力はありそうというか。
ただグローバルガバナンス的に、政府レベルで自由競争やっていいのかっていうのはあるけどな。前にレーガン大統領でそんなことなって地獄絵図だったらしいけど、もっと遡れば第二次世界大戦も自国経済さえなんとななりゃ知ったこっちゃねえやでブロック経済やって勃発したところあるしね。
まあ、とりあえず、私は群論が難しすぎてそれどころじゃないっす。法律学もそうだったけど、まず専門用語がわかりづらいんだよね。つーか、あえてわからないように作ってるだろ。やりなおし!!
剰余類
群Gに含まれる部分群Hに該当するすべての要素hと、群Gの要素であるaを作用させたもの。
aHなら左剰余類。Haなら右剰余類。
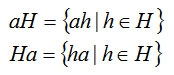
{}の中はaとhを作用させてて、hはHの要素だよということを示している。
ちなみに剰余類が作る
のような集合を商集合という。
正規部分群
剰余類において、hにaを左から作用させても、右から作用させても、結果がまったく変わらない場合、その部分群Hは正規部分群Nと呼ばれる。
剰余群
群Gにおける正規部分群Nの剰余類がつくる商集合G/Nがあったとき、その演算を(aN)(bN)=(ab)Nとすると、その商集合G/Nは群の公理をクリアーし群になる。これを剰余群という。
例題1
次の置換σの位数を求めよ。さらに剰余群S5/〈σ〉の位数を求めよ。
σ=
[12345]
[42531]∈S5
この置換は
1は4に
2は2のままで
3は5に
4は3に
5は1に
変えていってね!というルールなので
σ1=[12345]→[42531]
σ2=[12345]→[42531]→[32154]
σ3=[12345]→[42531]→[32154]→[52413]
σ4=[12345]→[42531]→[32154]→[52413]
→[12345]
と4ターンで元の数字の並びに戻ってくるので、σの位数は4。
剰余群S5/〈σ〉の位数は
S5の位数(要素の数)が5×4×3×2×1=120個なので
120/4=30である。
例題2
次の置換σの位数を求めよ。さらに剰余群S5/〈σ〉の位数を求めよ。
σ=
[12345]
[53214]∈S5
この置換は
1は5に
2は3に
3は2に
4は1に
5は4に
変えていってね!というルールなので
σ1=[12345]→[53214]
σ2=[12345]→[53214]→[42351]
σ3=[12345]→[53214]→[42351]→[13245]
σ4=[12345]→[53214]→[42351]→[13245]
→[52314]
σ5=[12345]→[53214]→[42351]→[13245]
→[52314]→[43251]
σ6=[12345]→[53214]→[42351]→[13245]
→[52314]→[43251]→[12345]
と6ターンで元の数字の並びに戻ってくるので、σの位数は6。
剰余群S5/〈σ〉の位数は
S5の位数(要素の数)が5×4×3×2×1=120個なので
120/6=20である。
例題3
3次対称群S3の部分群をすべて書き出し、正規部分群になるものとそうでないものに分類せよ。ちなみに対称群とは、ルービックキューブのように位置や順番を並び替える操作を元とする群のこと。
S3の元は
ι(イオタ。恒等置換)=[123]→[123]
σ1=[123]→[213]=(12)※動かした箇所
σ2=[123]→[321]=(13)
σ3=[123]→[132]=(23)
σ4=[123]→[231]=(123)※電光掲示板的に左ループ(1→2、2→3、3→1)
σ5=[123]→[312]=(132)※電光掲示板的に右ループ(1→3、3→2、2→1)
となる。
さてσ1の操作を2回するのと、σ2の操作を2回するのは、元に順番に戻るという意味で同じこと、という感じで
σ1²=σ2²=σ3²=ι
よって{ι、(12)}{ι、(13)}{ι、(23)}
は正規部分群(※恒等置換と等しい元と指数が2の元は正規部分群)。
同様に
σ4³=σ5³=ι
σ4²([123]→[231]→[312])=σ5([123]→[312])
σ5²([123]→[312]→[231])=σ4([123]→[231])
σ4σ5=σ5σ4=ι
より
{ι、(132)、(123)}も正規部分群。
またιとS3も定義上(どんな元を右から演算しても左から演算しても同じ)正規部分群。
したがってS3の正規部分群は
S3={ι、(12)、(13)、(23)、(123)、(132)}の6つ。