群論ってとにかく言葉がわかりづらい。つーかガロアの野郎わざとわかりづらく作りやがっただろ。そういうインテリふりかざすのいくない。だから隠れミッキー的に隠れトランプでてくる。
まあ、こういうところって初学者は厳密性よりも大まかなイメージが重要だと思うので、用語の定義を代数の式で表すよりも、できる限りわかりやすい文章で自分なりに記述してみました。ギリシャ文字の羅列なんていきなり見てもクリプトグラフィーよ。
互換
数と数、文字と文字の位置を交換すること。
偶奇(パリティ)
偶数か奇数かという意味。パリティーピーポー。
奇置換
互換の回数が奇数回。
偶置換
互換の回数が偶数回。
対称群(シンメトリックグループ)
位置や順番を並び替える操作を元とする群のこと。前回の例題のやつ。
絶対解けないケンちゃんパズル
ルービックキューブや、ケンちゃんラーメン新発売のパズルも対称群である。
あの手のスライドパズル(マスが4×4のものを15パズルという)はかつて外国でサム・ロイドというパズル職人がこんな感じの問題を作って1000ドルの賞金を懸けたことがある。
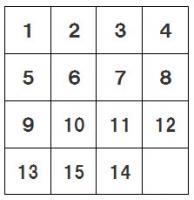
この状態から1~15を並び直せ、つまり15と14を置換しろっていう問題なんだけど、結論から言って、このパズルは絶対解けない。
これを解くには①15と14だけを並び変えて、さらに②空きマスの位置をそのままにしなければならないが、①の互換は奇数回、②の互換は偶数回行わないといけないので、どうやっても同時にできないのである。
空きマスの位置をそのままにするのがなんで偶数回の互換なのかというと、結局数と数とを交換するには空きマスをスライドさせなければならず、もとの位置に戻すには行きと帰りで往復(×2)しなくてはならないから。
交代群(オルタネーティンググループ)
対称群Sの偶置換に当たる元全てで構成される部分群のこと。
ケンちゃんラーメンでわかったように位置をキープするの(恒等置換ι)も偶置換なので交代群Aの元になる。
また、置換は偶数回と奇数回の二種類あるので、置換の合計nのちょうど半分が交代群の元の数となる。ちなみに奇置換のグループは恒等置換ができないので単位元を持たず、そのため群の公理をクリアできず群とならない。
さらに、交代群のすべての元は、対称群の任意の元に作用させることができ、その順序についても左から作用させても右から作用させても演算結果がまったく変わらないため、交代群は対称群の正規部分群であることがわかる。
例題
具体的に4次の対称群S4の交代群の元を考えてみる。
4次というのは文字や数字が4つ並んでいるということなので、その置換のパターンは4×3×2×1で24通り。
このうち半分が偶置換なので、交代群の元の数は以下の12個。
①[1234]→[1234](ι)
②[1234]→[2134]→[3124](123)
③[1234]→[3214]→[2314](132)
④[1234]→[2134]→[4132](124)
⑤[1234]→[4231]→[2431](142)
⑥[1234]→[3214]→[4213](134)
⑦[1234]→[4231]→[3241](143)
⑧[1234]→[1324]→[1423](234)
⑨[1234]→[1432]→[1342](243)
⑩[1234]→[2134]→[2143](12)、(34)
⑪[1234]→[3214]→[3412](13)、(24)
⑫[1234]→[4231]→[4321](14)、(23)
巡回群(サイクリックグループ)
一種類の元から生成される群。
例えば元Aからできる巡回群Cn=〈A〉は
{A-n…A-3、A-2、A-1、e、A1、A2、A3…An}
となる。
ここで巡回群の任意の二つの元をX、Yとすると
X=Am、Y=An(m、nは整数)
となるので
X・Y=Am・An=Am+n・・・①
Y・X=An・Am=Am+n・・・②
①、②より
X・Y=Y・X
したがって巡回群は交換法則が成り立つアーベル群。
有限巡回群
なぜ一種類の元から生成される群を巡回群と呼ぶのかイマイチよくわからなかったが、巡回群の元の数が有限個の場合、その理由がわかる。
元の数が決まっている場合は、際限なく演算を繰り返すとどこかで元の重複が起こるはずである。ラインナップの種類が決まっているガチャガチャやカードダスを無限に引けば遅かれ早かれダブりが出るようなものである。
重複が起きたときの演算回数をm、n(どちらも整数)とすると
Am=An
両辺にA-nをかけると
Am-n=An-n
Am-n=e
となり、Aをm-n回演算すると一周して単位元eに戻ってくることがわかる。
これが巡回群の由来・・・だと思う。
クラインの4元群
ちなみに4次の対称群S4の交代群の元のうち、単位元eと以下の3つの元でできる部分群をクラインの4元群という。ポークの名前ではない。
①[1234]→[1234](ι)
②[1234]→[2134]→[2143](12)、(34)
③[1234]→[3214]→[3412](13)、(24)
④[1234]→[4231]→[4321](14)、(23)
特徴として②~④の操作をそれぞれ2回行うと最初の順番に戻る。
例えば①→②や②→①は②と同じ。
同様に
①→③、③→①の操作は③の操作と同じ。
①→④、④→①の操作は④の操作と同じ。
※よってクラインの4元群は正規部分群。
また
②→③、③→②の操作は④の操作と一緒。
②→④、④→②の操作は③の操作と一緒。
③→④、④→③の操作は②の操作と一緒。
クラインの4元群は巡回群を除くと最も小さな群であり、構造主義のレヴィ=ストロースが『親族の基本構造』で使ったことでも有名。
写像
ふたつの別の群G1とG2の元がある関数Φ(ファイ)によってリンクしているとき、その関係を写像という。
写像であるためには二つの条件がある。
条件①:G1の任意の元は必ずG2の元のどれかに対応する。
条件②:G1の任意のひとつの元は、G2の複数の元には対応しない。※ただし超ややこしいけどその逆パターンはアリ。
単射
G1→G2の写像の際にG1の元がG2のたったひとつの元に対応していることをいう。
つまり1対1の関係。
全射
G1に属するすべての元がG2に写像されること。
同型写像
単射と全射を同時に満たす写像。
準同型写像
ある関数ΦがG1の元X1、Y1に作用するとき
Φ(X1Y1)=Φ(X1)Φ(Y1)=X2Y2
となるものを準同型写像という。
準同型写像はG1の元をG2の元、G1の単位元をG2の単位元に、G1の逆元をG2の逆元にそれぞれ送ってくれるため、群の構造を維持したまま別の群に移すという便利な性質があることが分かる。
核(カーネル)
式ではkerと表記される。「カーネル」とはフライドチキンではなくドイツ語で「コア」のこと。
G1→G2の写像の際にG2の単位元e2に写像されるG1の部分集合を指す。
ちなみに正規部分群は準同型写像の核である。
例題1
G1とG2を群、
e1とe2をそれぞれ単位元、
Φ:G1→G2を群の準同型写像、
準同型写像の核をKer(Φ)={g∈G1 |Φ(g)=e2}とする。
このとき、もしKer(Φ)={ e1 } ならばΦは単射であることを示せ。
そもそもG1→G2の写像の際にG2の単位元e2に写像されるG1の部分集合が核なので、G1の核がe1ならe1→e2なので、Φは単射。
例題2
Gをアーベル群、kを正の整数とするとき、次の写像Φは群の準同型写像であることを示せ。Φ:G→G1 Φ(g)=g^k
Φ(g)=g^k(kは整数)
Φ(g′)=g^l(lは整数)とすると
Φ(gg′)=g^(k+l)=g^k g^l=Φ(g)Φ(g′)
よって群の準同型写像である。
例題3
G1とG2を群、
e1とe2をそれぞれ単位元、
Φ:G1→G2を群の準同型写像、
準同型写像の核をKer(Φ)={g∈G1 |Φ(g)=e2}とする。
このとき、Ker(Φ)はG1の正規部分群であることを示せ。
まず、準同型写像ΦはG1の単位元をG2の単位元に移すので
Φ(e1)=e2
よってe1は準同型写像の核Ker(Φ)
e1∈Ker(Φ)・・・①(単位元がある)
と表せる。
X、YをKer(Φ)の任意の元とすると
G2の単位元e2に写像されるので
Φ(X)=Φ(Y)=e2
よって
Φ(XY)=Φ(X)Φ(Y)=e2e2
単位元同士を演算しても単位元のままなので
e2e2=e2
よって
XY∈Ker(Φ)・・・②(演算がとじる=ある群に属する元同士の演算結果もその群の元)
また、XをKer(Φ)の任意の元とすると
Φ(X)=e2なので
その逆元も
Φ(X-1)=e2^(-1)=e2
よって
X-1∈Ker(Φ)・・・③(逆元がある)
①~③よりKer(Φ)はG1の部分群の条件をクリアーする。
さらに、XをKer(Φ)の任意の元、gをG1の任意の元とすると
Φ(g X g-1)=Φ(g)Φ(X)Φ(g-1)
※Φ(X)=e2より
Φ(g)Φ(X)Φ(g-1)=Φ(g) e2 Φ(g-1)=Φ(g)Φ(g-1)=e2
よって、(gX g-1)∈Ker(Φ)
以上から、Ker(Φ)はG1の正規部分群である。
例題4
G1G2を群
Φ:G1→G2を群の準同型写像
核の写像先の値域(イミッジ)をIm(Φ)={Φ(g)|g∈G1}⊂G2
とする。
このときIm(Φ)はG2の部分群であることを示せ。
Φ(g)、Φ(g′)∈Im(Φ)とする。
Φ(g)Φ(g′)^-1=Φ(gg′^-1)∈Im(Φ)
よってIm(Φ)はG2の部分群である。