もう、いきなり言葉が特殊でわかりにくい。同じような言葉を別の分野ではこう言うよねっていうのがあって。例えば、汎化っていうよりは一般化とかの方がメジャーな表現だと思うわけよ。オブジェクトって表現もあまりピンと来ないんだよな。英語圏の人はスッと入るんだろうけれど。
というか、最近のビジネス業界のなんでもカタカナにしときゃいいんだ的風潮が本当に腹が立つ。グロスを総計と言わない理由には何かあるのかい??レジャーもそうだよ、アクティビティとかコンセッションとかよ。やっぱり外資系の圧力なのかね??
例えば、コミュニケーションとか日本語にないワードならばいいんだけど、上手く日本語に訳せる言葉ですらカタカナ使っているのがなあ・・・しかも、なんか、使っている奴が大抵得意げなのもムカつくよなwまあ、その権化が小池百合子さんだと思うよ。
参考文献:内山俊郎著『わかりやすい情報システムの設計』
未来を予測する最善の方法は、未来を発明することである。――アラン・ケイ(オブジェクト指向のパイオニア)
システム
複数の要素が有機的に関係しあい、全体としてまとまった機能を発揮している要素の集合体。組織、系統、仕組み。
つまり、構成要素がてんでバラバラに、それぞれ好き勝手に働いているものはシステムではない。
いいシステムの条件
不具合が生じた時には、システムの構成要素を修正する必要があるが、その時にできるだけ修正範囲を限定でき、修正すべき内容が理解しやすいシステムがいいシステムだとされる。
オブジェクト指向は以下のよいシステムの条件が実現しやすいと言われている。
条件①疎結合性
システムの構成要素同士の結合度が低い(複雑になりすぎるので、あんまりなんでもかんでも結び付けない)。
条件②高凝集性
直感的に理解しやすい抽象性を持つ(全部具体的に書かない)。
エンジニアは顧客の要求通りのシステムは作ってはいけないというのは笑った。
理由は、①顧客は作るべきシステム要件を全て知らないから。②顧客は作るべきでない要求をする可能性があるから。
こういうのって、ダメな上司の命令とかもありそうだよな。で、うまくいなして、部下たちが勝手にフォローしちゃうっていうね。
UML
ユニファイド・モデリング・ラングエージ。統一モデリング言語。
システムの構造を分かりやすく図で示す統一された方法のこと。80年代~90年代初頭には、紛らわしいローカルルールがたくさん存在したため、オブジェクト指向プログラミング言語の標準化に乗り出したという経緯がある。
クラス
データ(属性)と処理(操作)をセットにしたもの。
例えばAというグループに分類できるデータは処理Aが行うといったようにすること。これによりシステムがわかりやすくなる。
UMLでは

といった図で表す。
インスタンス(オブジェクト)
実体。クラスによって作られる値。
粉物を例にすると、クラスがたい焼き器、インスタンスがたい焼き。
これがクラスがたこ焼き器になると、インスタンスはたい焼きではなくたこ焼きができる。
UMLでは
と二段の長方形で描く。インスタンス名をクラス名より先に記述するのに注意。
また、クラスのUMLと区別するために、インスタンスのクラス名やインスタンス名には必ず下線を引く。
ちなみにクラス名のみ記述する場合は
と:を残す。
また、属性すら省略する場合は
とする。
サブクラス
会員における特別会員など。ベン図などの集合の考え方をすると理解しやすい。
逆に言うと、特別会員を汎化したものが会員なので、特別会員 → 会員 と矢印で記述する。
※矢印の形は本当は正三角形に直線。これは正しく書かなければならない。
関連
クラスとクラスが関連している場合、そのクラスどうしを実線で結び、その端には、関連先に結びつくインスタンスの数(多重度)を示す。
多重度(カーディナリティ)の記述の仕方は以下のとおり。
0..1 0か1
1 1だけ(5とかけば5だけ)
1..* 1以上(2..*と書けば2以上)
* 0以上(ならなんでもいい)
例えば、購入者というクラスと、購入というクラスと、タイトルというクラスがあった場合、ある特定の購入があった場合を考えると、購入者は一人に、購入された書籍のタイトルは一冊に特定できるので、クラス関連図は以下のようになる。
※逆にある購入者がいたとき、その人が行った本の購入は(よほどの活字アレルギーでもない限り)複数回あるため、購入のクラス側には*を用いている。
このように、関連図は中央に出来事(用言)のクラス、両端に人や物(体言)のクラスが来ることが多い。
多重度の演習
多重度の入れ方がかなり難しい問題。
生徒が20人いて、生徒が受講できる講義の科目が10科目あるとする。生徒、受講、講義科目の3つのクラスを作り、これらの関係図を作りなさい。
なお、1つも講義を受講しない生徒や、一人も生徒が受講しない講義があっても良いとする。
解答例
一人の生徒から見て、その生徒が受講する科目の数は最低で0科目、最大で10科目なので、左側の多重度が0..10となり、逆にある講義科目から見て、その講義科目を受講する生徒は最低で0人、最大で20人なので、右側の多重度は0..20となるのである。
インタフェース
境界面という意味。抽象クラスと近いが、仕様の定義(抽象操作の宣言)のみを行なうため、インタフェースからインスタンスは作れない。
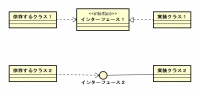
つまり、インタフェースには具体的な実体がないので、実体化するためにはほかのクラスに実装してもらう必要がある。その場合は三角形付きの点線矢印で結ぶ。
また、あるクラスがインタフェースを使用する場合を図で表す場合は、両者を依存関係を表す点線の矢印で結ぶ。
また、インタフェースにはもうひとつ表現の仕方があって、それはロリポップ(キャンディ)という円で示す方法なのだが、この場合は実装関係が実線になるので注意!