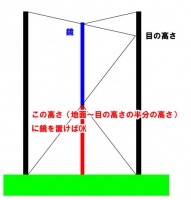
全身鏡で、ある高さの人の全身が写るようにするには、その鏡をどれくらいの高さに設置すればいいかという問題があるが、これは、地面から目の高さまでの距離を半分にした高さが正解。
ちなみに、この関係は鏡との距離に関わらないため、全身鏡の高さは使う人の身長の半分以上は必ずないといけないことになる。
屈折率
空気中(媒質1)→水(媒質2)、水(媒質2)→空気中(媒質1)で屈折角の位置が変わるのがややこしい(屈折の大きさはもちろん一緒)。
屈折率n12=媒質1の入射角の大きさ(=sinα)/媒質2の屈折角の大きさ(=sinβ)
音階周波数
オーケストラではドレミの「ラ」の音を基準にチューニングを行うという。
理科的には「ラ」の周波数は440Hzジャストだが、ヨーロッパ(ウィーン交響楽団など)では444Hzでチューニングされたり、バロック時代後期では392Hzと低かった。ちなみに現代の日本の基準は442Hzだという。
1オクターブ音を上げるには、弦の振動数fを2倍にする必要があり、振動数は弦の長さL、張力T、線密度ρ(※弦によって決まる定数)によって以下の式のように決まる。
f=(1/2L)×√(T/ρ)
つまり、fを2倍にするには張力を4倍、もしくは弦の長さを半分にしなければならない。
打楽器と吹奏楽器
コップを棒で叩く場合は、コップに入っている水の量が多いほど低い音が出る。これは、コップそのものが振動するため、水の量が多いほどコップの重量が重くなり、遅く振動するから。
試験管の縁に唇を当てて吹いた場合は、水の量が多いほど高い音が出る。これは、試験管の中の空気が振動するため、水の量が大きくなるほど空気の体積が少なくなり、速く振動するから。















