でも、javaでプログラミングする第5講あたりから、まずもってjavaがやれる環境を準備するのが大変で、ソフトウェアとか3つくらい必要だし、そこでかなり労力を使っちまったよ。
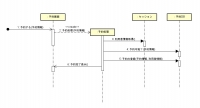
シーケンス図
あるシステムの処理において、それぞれのオブジェクトがどのように協調・影響し合うかを、時間軸に沿って説明する図。
各オブジェクトの関係はコミュニケーション図という図でも表せるが、その場合時間経過は表現できない。
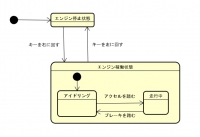
ステートマシン図
図書館にある本の状態(書架にある・貸し出し中)など、システムの振る舞いを記述するための図。開始状態を黒い丸、状態は角が丸い枠で表す。
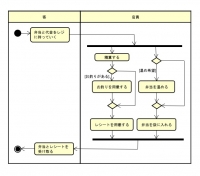
アクティビティ図
動的な処理の流れを表現できる図で、フローチャートに似ている。
条件判断や並列処理を表現する際に用いられる。
処理全体の流れをおおまかに表現したい場合はアクティビティ図、もう少し個々の相互作用のディティールも表現したい場合はシーケンス図など、使い分けが大切らしい。
各ノードは次のとおり。
開始ノード:黒い丸。システムの開始を表す。
ディシジョンノード:菱形。分岐点を表す。
マージノード:菱形。集合点を表す。
フォークノード:太い横線。並列処理の開始を表す。
ジョインノード:太い横線。並列処理の終了を表す。
終了ノード:黒い二重丸。システムの終了を表す。
また、「顧客」「店員」「店長」のように、アクションをする人や組織ごとに、アクションのグループ分けをすることができる(アクティビティ・パーティション)。
javaプログラミング演習
事前にJDK(ジャヴァ・デベロップメント・キット)というソフトウェアをダウンロードしたあと、システムのプロパティのコーナーにある「環境変数の設定」の「path」にJDKがダウンロードされた所在地のアドレス(ただしセミコロン;とbinで挟む!!)を追加する。
さらにjEditというソフトウェアもダウンロードするのだが、拡張子がマックでしか通用しないタイプ(.dmg)で、開くのに結構手間がかかる(´;ω;`)
この準備が終わったら、どこでもいいので、ある任意のフォルダを作って、そのフォルダに課題のソースコードのファイルをぶち込む。
次に課題が入ったファイルをマウスポインタで選択したあと、シフトキーを押しながら右クリックをすると、コマンドウィンドウをここで開くという、通常出てこない選択肢が出てくる。
これを選ぶと、選択したフォルダ(ディレクトリ)のコマンド入力画面が出てくるので、ここで、jEdit ソースコード名 と半角で入力する。これで、ウィンドウズのソースコード入力ツールであるjEditの入力画面に飛んでくれる。
ちなみに、OSがリナックスだとgeditという別のエディタになる。
メソッド
javaの世界では操作はメソッドと呼ばれる。"main"というメソッドだけは、コマンドウィンドウから起動および実行できる。
astah* professionalとの関連
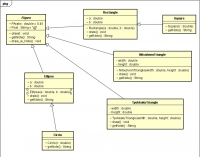
すごい便利なのが、クラス図などの描画ソフト「アスタープロフェッショナル」でjavaのソースコードが読み込めるという点。javaのコードをそのまま図に変換してくれる。
手順は、「ツール」→「java」→「javaソースコードの読み込み」→好きなファイルを選択→図にしたいデータを候補リストから選択リストに移す→「了解」
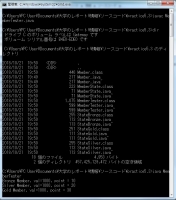
上のソースコードをこんな感じで自動的に描画してくれる。素敵。
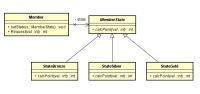
リバースエンジニアリング
設計書からプログラムを作ることをフォワードエンジニアリングというが、それの逆。
つまりプログラムから設計書を作ること。
javaで作図をする
懐かしのプログラミング基礎が思い出されずにはいられない課題。
特に、楕円とか二等辺三角形の数式が激ムズ。
ただ思ったのは、C言語って汎用性が高いなというか、文法はほとんどCもjavaも変わらないのねっていう。
図形の設定コード(Figure)
abstract class Figure{
final double PAratio = 0.45; // 画素のアスペクト比
final String Pixel = "@"; // 図形は@の集合として描けという意味
abstract void draw();
abstract String getNote();
void draw_w_Note(){
draw(); // ←描画は文章の前に描き出させる
System.out.println("上記の図形は,"+getNote());
}
}
直角三角形の作図コード(TyokkakuTriangle)
class TyokkakuTriangle extends Figure{
private double width; // 直角三角形の幅
private double height; // 直角三角形の高さ
TyokkakuTriangle( double width, double height ){
this.width = width;
this.height = height;
}
void draw() {
for( double i = 0 ; i < height ; i++ ){
for( double j = 0 ; j < width/PAratio ; j++ ){
double x = (j + 0.5)*PAratio;
double y = height - 0.5 - i;
double equation = y + height/width*x - height;
if( equation <=0 ) System.out.print(Pixel);
else System.out.print(' ');
}
System.out.println();
}
}
String getNote(){
return "底辺、高さが(" + this.width + ", " + this.height+ ")の直角三角形"; }
}
二等辺三角形の作図コード(NitouhennTriangle)
class NitouhennTriangle extends Figure{
private double width; // 二等辺三角形の幅
private double height; // 二等辺三角形の高さ
NitouhennTriangle( double width, double height ){
this.width = width;
this.height = height;
}
void draw() {
for( double i = 0 ; i < height ; i++ ){
for( double j = 0 ; j < width/PAratio ;j++ ){
double x = (j + 0.5) * PAratio;
double y = height - 0.5 - i;
double equation1 = y + 2.0*height/width*x - 2.0*height;
double equation2 = y - 2.0*height/width*x;
if( equation1 <=0 && equation2 <=0 ) System.out.print(Pixel);
else System.out.print(' ');
}
System.out.println();
}
}
String getNote(){
return "底辺、高さが(" + this.width + ", " + this.height+ ")の二等辺三角形"; }
}
図形の呼び出しコード(FigureTester)
このソースをコマンドプロンプトでコンパイルすると全部引っ張り出される。
ちなみに、コンパイルの仕方は「javac FigureTester.java」→「java FigureTester」でOK。
class FigureTester{
public static void main(String[] args){
TyokkakuTriangle myTyokkakuTriangle = new TyokkakuTriangle(5,10);
myTyokkakuTriangle.draw_w_Note();
NitouhennTriangle myNitouhennTriangle = new NitouhennTriangle(19,15);
myNitouhennTriangle.draw_w_Note();
}
}
コンパイル例
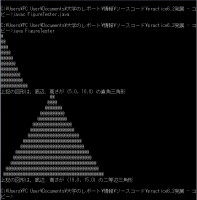
リバースエンジニアリング