遺伝の法則が解明されていくに従って、ダーウィンの進化論はどんどん旗色が悪くなっていくのだが、実はメンデル一派もとある壁にぶち当たっていた。
それはコロンビア大学のトーマス・モーガンの実験から始まる・・・モーガンはショウジョウバエという小バエを何も手を加えずに自然な環境で何世代にもわたって飼育し続けた。
するとオオマツヨイグサのように、ある時目の色が普通(=普通は赤い)とは違う、白い目のショウジョウバエの個体が現れた。
この時(1907年)からモーガンは突然変異のメカニズムの研究にハマりだした。一体どのように遺伝情報が変化し突然変異がもたらされるのか・・・
モーガンは飼育中のショウジョウバエたちの膨大な形質を根性で記録。そして形質の変化に、細胞の核にある染色体が関係している可能性を考えだした。
当時はワイズマンが生殖質連続質を研究していたこともあり、生殖細胞を介して遺伝情報が引き継がれる事は分かっていた。
だが遺伝情報が細胞のどこにあるのかは大きな謎だった。細胞質にあるんじゃないか?という説もあったのだが、モーガンは通常のショウジョウバエの染色体と、突然変異体のショウジョウバエの染色体の形が異なっている事、そしてショウジョウバエの目の色の突然変異は性別に大きく関わっている(伴性遺伝)事を発見し、性別の決定は染色体に関係していることから、遺伝子は染色体の中にあると考えたのだ。
またモーガンの弟子ハーマン・マラーはショウジョウバエに放射能を当てることで、人為的に突然変異を誘発できることを明らかにした。
・・・したのだが、ここで現れる突然変異体は羽根が縮んだり、羽根が無くなったり、触覚が無くなったり、適応において有利に働くとは思えない変化ばかりであった。
果たして突然変異は本当に進化の原動力なのか・・・?
28.突然変異VS自然選択説
2010-11-30 01:41:27 (15 years ago)
-
カテゴリタグ:
- 進化論
突然変異・・・この言葉は結構有名だ。突然変異と言うのはその言葉通り、突然生物の形質が変わってしまうことだ。
これは「黄色と種皮の親」から「黄緑の種皮の子」が生まれたり、赤いバラから、突然青いバラが生まれることを意味する。オランダ人もびっくり。
そしてそれは遺伝性・・・つまりその形質を決める遺伝情報そのものが変わってしまい、それが新たな形質を生んでいる事になる。
この現象に初めて注目したのが、ワイズマンのところで少しふれたが、オランダのド・フリースだ。
ド・フリースは、オオマツヨイグサという花を栽培中、その中に親と全く異なる、とんでもなくデカイ花をつけた子を見つけた。
これは別に愛人との訳ありの子・・・とかそういう話じゃない。まぎれもなく普通の花の大きさの親同士から生まれた子である。勘ぐっちゃダメ!
この突然変異の概念は、いつまでたっても新しい形質が出来なかったメンデルの遺伝の法則を増強し、進化のメカニズムと言うのは、ダーウィンの言うように連続的でゆっくり時間をかけて起こるのではなく非連続的で、とある世代交代において突然瞬時に起こるという説が主流になった。
これは「黄色と種皮の親」から「黄緑の種皮の子」が生まれたり、赤いバラから、突然青いバラが生まれることを意味する。オランダ人もびっくり。
そしてそれは遺伝性・・・つまりその形質を決める遺伝情報そのものが変わってしまい、それが新たな形質を生んでいる事になる。
この現象に初めて注目したのが、ワイズマンのところで少しふれたが、オランダのド・フリースだ。
ド・フリースは、オオマツヨイグサという花を栽培中、その中に親と全く異なる、とんでもなくデカイ花をつけた子を見つけた。
これは別に愛人との訳ありの子・・・とかそういう話じゃない。まぎれもなく普通の花の大きさの親同士から生まれた子である。勘ぐっちゃダメ!
この突然変異の概念は、いつまでたっても新しい形質が出来なかったメンデルの遺伝の法則を増強し、進化のメカニズムと言うのは、ダーウィンの言うように連続的でゆっくり時間をかけて起こるのではなく非連続的で、とある世代交代において突然瞬時に起こるという説が主流になった。
27.メンデルの遺伝の法則では進化は起きない?
2010-11-30 01:37:18 (15 years ago)
-
カテゴリタグ:
- 進化論
メンデルの遺伝の法則において重要な考えが対立形質というものだ。これはその名の通り「対をなしている生物の形質のこと」であり、それは生物の対立形質ごとに独立している。
これをメンデルの独立の法則という(え?連鎖があるって?その話は後回しにさせてください)。
たとえば、メンデルがハマったエンドウで言うと・・・種子の形の対立形質は「まる」か「しわ」だし、種皮の色は「黄色」か「緑」、鞘の形は「ふっくら」か「くびれ」とそれぞれ決まっていて、「種皮が黄色のエンドウは、種子を必ずしわにする」といった種皮の色の決定が、種子の形の決定に影響を及ぼすことはない。(え・・・?染色体の連鎖??ワタシニホンゴワカラナイ・・・)
そして「黄色と種皮の親」と「緑の種皮の親」を交雑すると、色が混じりあって「黄緑の種皮の子」が生まれる・・・と言うのではなく子どもの種皮はいつでも黄色か緑かのどちらかなのだ。
ダーウィンの進化論は「形質が世代交代ごとに徐々に変化していき、それが結果的に大きな変化になって現れる」というものだったが、このメンデルの法則はそれに反する。
なぜならメンデルの遺伝の法則では、異なる形質を交雑しても、新たな形質は生まれないからだ。
変化するのは、独立した対立形質の組み合わせだった。それは「黄色」「しわ」「ふっくら」のエンドウや、「黄色」「まる」「くびれ」エンドウ、「緑」「まる」「ふっくら」エンドウと言ったように・・・
では一体全体「キリンの長い首」のような、今までなかった新しい形質はどのように生まれるのだろうか??
これをメンデルの独立の法則という(え?連鎖があるって?その話は後回しにさせてください)。
たとえば、メンデルがハマったエンドウで言うと・・・種子の形の対立形質は「まる」か「しわ」だし、種皮の色は「黄色」か「緑」、鞘の形は「ふっくら」か「くびれ」とそれぞれ決まっていて、「種皮が黄色のエンドウは、種子を必ずしわにする」といった種皮の色の決定が、種子の形の決定に影響を及ぼすことはない。(え・・・?染色体の連鎖??ワタシニホンゴワカラナイ・・・)
そして「黄色と種皮の親」と「緑の種皮の親」を交雑すると、色が混じりあって「黄緑の種皮の子」が生まれる・・・と言うのではなく子どもの種皮はいつでも黄色か緑かのどちらかなのだ。
ダーウィンの進化論は「形質が世代交代ごとに徐々に変化していき、それが結果的に大きな変化になって現れる」というものだったが、このメンデルの法則はそれに反する。
なぜならメンデルの遺伝の法則では、異なる形質を交雑しても、新たな形質は生まれないからだ。
変化するのは、独立した対立形質の組み合わせだった。それは「黄色」「しわ」「ふっくら」のエンドウや、「黄色」「まる」「くびれ」エンドウ、「緑」「まる」「ふっくら」エンドウと言ったように・・・
では一体全体「キリンの長い首」のような、今までなかった新しい形質はどのように生まれるのだろうか??
26.遺伝の法則のパラドクス
2010-11-30 01:28:05 (15 years ago)
-
カテゴリタグ:
- 進化論
ダーウィンの自然選択説のポイントは、小さな形質の変化が世代交代を繰り返すことで、その種の形質に大きな変化をもたらすということだ。
しかしこの理論には当時大きなアキレス腱があった。この世代交代ごとの小さな形質の変化についてのメカニズムがダーウィンにも解らなかったのだ。
つまりこれは遺伝の法則のことである。
遺伝はダーウィンの進化論の中核をなす重要なポイント。その仕組みがよく分からないのでは、進化論の説得力が大きく低下してしまう・・・
一応父親と母親の形質情報(遺伝子)をそれぞれ半分ずつ子どもが受け継ぐとは、ダーウィンも考えてはいた。
そしてこの考え自体は正しい。しかしこの理論を自然選択説に応用すると矛盾を抱えてしまう。どういうことかと言うと、ある世代に現れた新しい形質が、世代交代をするたびにどんどん薄まっていってしまうのだ(詳しくは図を参照)。
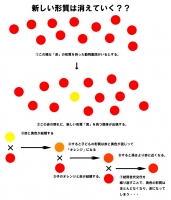
この考えでは何回世代交代を重ねても赤の群れが黄色の群になることはない。しかしこれに矛盾しない遺伝の法則は、実は『種の起源』発行のたった7年後(1866年)にチェコの修道士によって考えられていた。
・・・考えられてはいたのだが、その理論の重要性に気付く人間はダーウィンはおろか
この時誰もいなかった・・・
メンデルの遺伝の法則・・・これが脚光を浴びるのは1900年・・・なんと34年後のことだった。この時ダーウィンも、称賛されるべき遺伝法則の父メンデルもとっくに死んでいた・・・
しかしこの理論には当時大きなアキレス腱があった。この世代交代ごとの小さな形質の変化についてのメカニズムがダーウィンにも解らなかったのだ。
つまりこれは遺伝の法則のことである。
遺伝はダーウィンの進化論の中核をなす重要なポイント。その仕組みがよく分からないのでは、進化論の説得力が大きく低下してしまう・・・
一応父親と母親の形質情報(遺伝子)をそれぞれ半分ずつ子どもが受け継ぐとは、ダーウィンも考えてはいた。
そしてこの考え自体は正しい。しかしこの理論を自然選択説に応用すると矛盾を抱えてしまう。どういうことかと言うと、ある世代に現れた新しい形質が、世代交代をするたびにどんどん薄まっていってしまうのだ(詳しくは図を参照)。

この考えでは何回世代交代を重ねても赤の群れが黄色の群になることはない。しかしこれに矛盾しない遺伝の法則は、実は『種の起源』発行のたった7年後(1866年)にチェコの修道士によって考えられていた。
・・・考えられてはいたのだが、その理論の重要性に気付く人間はダーウィンはおろか
この時誰もいなかった・・・
メンデルの遺伝の法則・・・これが脚光を浴びるのは1900年・・・なんと34年後のことだった。この時ダーウィンも、称賛されるべき遺伝法則の父メンデルもとっくに死んでいた・・・
25.ダーウィニズム論争勃発!
2010-11-30 01:06:18 (15 years ago)
-
カテゴリタグ:
- 進化論
とにかく『種の起源』の内容におかんむりだったのが教会関係者だ。オックスフォードの学会ではダーウィンの理論は彼らの猛批判に合い、なんて可哀想なダーウィン・・・んん?
ダーウィンが会場にいないぞ!
・・・あの~ダーウィンさんの学説を議論しているのに、ダーウィンさんはどこにいるんですか?ええ?家!?さすが引きこもりのダーウィン!やってくれるぜ!
じゃあ、教会関係者に対して、自然選択説を猛烈に擁護してくれているあの人は誰?その人こそ「ダーウィンの番犬」の二つ名を持ち、19世紀最高の生物学者ともいわれるトマス・ヘンリー・ハクスリーだった。
オッカムの剃刀とその知名度で、ハクスリーはダーウィンに代わって頭の固い教会関係者と激しく戦い続けた。
その論戦の様子を家で「へ~そうだったんだ~」とダーウィンは呑気に聞いていた。
ちなみに「世界はダーウィンが思っているほど長くはない!4004年だ!」という教会側の反論に対しては先輩の地質学者ライエルが力を貸してくれた。
・・・とはいえハクスリーやライエルに反論の全てをまる投げしていたわけではない。
動物学者たちの的確な批判については、ダーウィン自身が逃げずにしっかりと論理的に回答している。
ドイツやスイスの動物学者の質問
Q.植物の種の形とか、ぱっと見、その生物の何の役に立っているか分からない。これがなんで自然選択で獲得されたって言えるのか?
ダーウィンの答え
A.昔役に立ってたんじゃない?あと一見していらなそうな器官でも、他の器官が影響を受けたり、見た目とは違った働きをしているのかもしれない。
イギリスの動物学者の質問
Q.キリンの長い首は、高い所の餌を食べるための有利な形質だというが、それに伴い体が大きくなっちゃえば、食べる量が増えるわけで本当に有利な形質だとは言えないのではないか?
ダーウィンの答え
A.キリンと同じ地域にキリンくらい大きく高い所の餌を食べられる動物がいたんじゃない?その動物よりも高い餌を食べることがキリンにとって有利だったのかもしれない。
また「ある種が徐々に変化して、別の種に進化するならば、その変化の過程の中間種(首が中くらいの長さのキリンなど)が見つからないのはなぜか?」という有名な疑問に対しては、ダーウィン運が良かった。
爬虫類と鳥類のちょうど中間の特徴を併せ持つ始祖鳥がドイツで発掘。この始祖鳥の化石は進化論をなかったことにしたい闇の組織によってクチバシから歯が抜かれてしまったが、この鳥には翼に鉤爪を備えた指も生えていた。
また脚の短いウマ、体が小さく、鼻の短いゾウなどの化石も見つかった。
ダーウィンが会場にいないぞ!
・・・あの~ダーウィンさんの学説を議論しているのに、ダーウィンさんはどこにいるんですか?ええ?家!?さすが引きこもりのダーウィン!やってくれるぜ!
じゃあ、教会関係者に対して、自然選択説を猛烈に擁護してくれているあの人は誰?その人こそ「ダーウィンの番犬」の二つ名を持ち、19世紀最高の生物学者ともいわれるトマス・ヘンリー・ハクスリーだった。
オッカムの剃刀とその知名度で、ハクスリーはダーウィンに代わって頭の固い教会関係者と激しく戦い続けた。
その論戦の様子を家で「へ~そうだったんだ~」とダーウィンは呑気に聞いていた。
ちなみに「世界はダーウィンが思っているほど長くはない!4004年だ!」という教会側の反論に対しては先輩の地質学者ライエルが力を貸してくれた。
・・・とはいえハクスリーやライエルに反論の全てをまる投げしていたわけではない。
動物学者たちの的確な批判については、ダーウィン自身が逃げずにしっかりと論理的に回答している。
ドイツやスイスの動物学者の質問
Q.植物の種の形とか、ぱっと見、その生物の何の役に立っているか分からない。これがなんで自然選択で獲得されたって言えるのか?
ダーウィンの答え
A.昔役に立ってたんじゃない?あと一見していらなそうな器官でも、他の器官が影響を受けたり、見た目とは違った働きをしているのかもしれない。
イギリスの動物学者の質問
Q.キリンの長い首は、高い所の餌を食べるための有利な形質だというが、それに伴い体が大きくなっちゃえば、食べる量が増えるわけで本当に有利な形質だとは言えないのではないか?
ダーウィンの答え
A.キリンと同じ地域にキリンくらい大きく高い所の餌を食べられる動物がいたんじゃない?その動物よりも高い餌を食べることがキリンにとって有利だったのかもしれない。
また「ある種が徐々に変化して、別の種に進化するならば、その変化の過程の中間種(首が中くらいの長さのキリンなど)が見つからないのはなぜか?」という有名な疑問に対しては、ダーウィン運が良かった。
爬虫類と鳥類のちょうど中間の特徴を併せ持つ始祖鳥がドイツで発掘。この始祖鳥の化石は進化論をなかったことにしたい闇の組織によってクチバシから歯が抜かれてしまったが、この鳥には翼に鉤爪を備えた指も生えていた。
また脚の短いウマ、体が小さく、鼻の短いゾウなどの化石も見つかった。
- Calendar
<< January 2026 >> Sun Mon Tue Wed Thu Fri Sat 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
- search this site.
- tags
-
- 漫画 (387)
- 脚本 (243)
- 映画 (235)
- 雑記 (163)
- ゲーム (156)
- 本 (116)
- 教育 (107)
- 生物学 (105)
- 科学 (93)
- 社会学 (81)
- 歴史 (72)
- テレビ (71)
- 芸術 (61)
- 政治 (50)
- 数学 (40)
- 進化論 (40)
- 資格試験 (38)
- 情報 (38)
- サイト・ブログ (37)
- 語学 (37)
- 映画論 (36)
- 物理学 (33)
- 哲学 (32)
- 恐竜 (29)
- 育児 (28)
- 文学 (26)
- 化学 (25)
- 論文 (22)
- PIXAR (22)
- 心理学 (18)
- 地学 (16)
- 気象学 (15)
- 地理学 (15)
- 技術 (13)
- 経済学 (12)
- 医学 (11)
- 玩具 (9)
- 司書 (8)
- 法律学 (7)
- 対談 (5)
- スポーツ (4)
- 映画の評価について (1)
- プロフィール (1)
- archives
-
- 202601 (2)
- 202512 (4)
- 202511 (15)
- 202510 (8)
- 202509 (5)
- 202508 (3)
- 202507 (3)
- 202506 (3)
- 202505 (1)
- 202504 (2)
- 202503 (2)
- 202502 (2)
- 202501 (1)
- 202412 (2)
- 202411 (6)
- 202410 (2)
- 202409 (4)
- 202408 (4)
- 202407 (7)
- 202406 (27)
- 202405 (11)
- 202404 (4)
- 202403 (23)
- 202402 (22)
- 202401 (15)
- 202312 (4)
- 202311 (7)
- 202310 (2)
- 202309 (8)
- 202308 (9)
- 202307 (8)
- 202306 (5)
- 202305 (15)
- 202304 (4)
- 202303 (4)
- 202302 (2)
- 202301 (4)
- 202212 (15)
- 202211 (7)
- 202210 (5)
- 202209 (4)
- 202208 (4)
- 202207 (7)
- 202206 (2)
- 202205 (5)
- 202204 (3)
- 202203 (2)
- 202202 (5)
- 202201 (6)
- 202112 (6)
- 202111 (4)
- 202110 (6)
- 202109 (7)
- 202108 (5)
- 202107 (8)
- 202106 (4)
- 202105 (8)
- 202104 (4)
- 202103 (6)
- 202102 (10)
- 202101 (3)
- 202012 (12)
- 202011 (3)
- 202010 (4)
- 202009 (5)
- 202008 (6)
- 202007 (4)
- 202006 (4)
- 202005 (4)
- 202004 (7)
- 202003 (5)
- 202002 (6)
- 202001 (8)
- 201912 (6)
- 201911 (5)
- 201910 (3)
- 201909 (4)
- 201908 (10)
- 201907 (3)
- 201906 (6)
- 201905 (10)
- 201904 (3)
- 201903 (7)
- 201902 (8)
- 201901 (5)
- 201812 (7)
- 201811 (12)
- 201810 (7)
- 201809 (5)
- 201808 (10)
- 201807 (5)
- 201806 (19)
- 201805 (14)
- 201804 (11)
- 201803 (15)
- 201802 (4)
- 201801 (6)
- 201712 (4)
- 201711 (3)
- 201710 (11)
- 201709 (9)
- 201708 (15)
- 201707 (7)
- 201706 (4)
- 201705 (5)
- 201704 (6)
- 201703 (7)
- 201702 (6)
- 201701 (3)
- 201612 (3)
- 201611 (7)
- 201610 (7)
- 201609 (2)
- 201608 (8)
- 201607 (8)
- 201606 (7)
- 201605 (3)
- 201604 (4)
- 201603 (8)
- 201602 (3)
- 201601 (2)
- 201512 (3)
- 201511 (3)
- 201510 (4)
- 201509 (4)
- 201508 (8)
- 201507 (17)
- 201506 (2)
- 201505 (5)
- 201504 (9)
- 201503 (20)
- 201502 (7)
- 201501 (4)
- 201412 (5)
- 201411 (3)
- 201410 (2)
- 201409 (3)
- 201408 (3)
- 201407 (3)
- 201406 (12)
- 201405 (6)
- 201404 (7)
- 201403 (5)
- 201402 (12)
- 201401 (9)
- 201312 (6)
- 201311 (9)
- 201310 (8)
- 201309 (6)
- 201308 (6)
- 201307 (6)
- 201306 (10)
- 201305 (10)
- 201304 (23)
- 201303 (17)
- 201302 (16)
- 201301 (5)
- 201212 (10)
- 201211 (4)
- 201210 (18)
- 201209 (4)
- 201208 (30)
- 201207 (7)
- 201206 (4)
- 201205 (6)
- 201204 (4)
- 201203 (4)
- 201202 (3)
- 201201 (3)
- 201112 (4)
- 201111 (7)
- 201110 (3)
- 201109 (9)
- 201108 (3)
- 201107 (7)
- 201106 (2)
- 201105 (11)
- 201104 (7)
- 201103 (14)
- 201102 (19)
- 201101 (27)
- 201012 (25)
- 201011 (70)
- 201010 (34)
- 201009 (30)
- 201008 (42)
- 201007 (44)
- 201006 (29)
- 201005 (37)
- 201004 (50)
- 201003 (44)
- 201002 (48)
- 201001 (38)
- 200912 (20)
- recent trackback
- others
-
- RSS2.0
- hosted by チカッパ!
- HEAVEN INSITE(本サイト)


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 | 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 | 121 | 122 | 123 | 124 | 125 | 126 | 127 | 128 | 129 | 130 | 131 | 132 | 133 | 134 | 135 | 136 | 137 | 138 | 139 | 140 | 141 | 142 | 143 | 144 | 145 | 146 | 147 | 148 | 149 | 150 | 151 | 152 | 153 | 154 | 155 | 156 | 157 | 158 | 159 | 160 | 161 | 162 | 163 | 164 | 165 | 166 | 167 | 168 | 169 | 170 | 171 | 172 | 173 | 174 | 175 | 176 | 177 | 178 | 179 | 180 | 181 | 182 | 183 | 184 | 185 | 186 | 187 | 188 | 189 | 190 | 191 | 192 | 193 | 194 | 195 | 196 | 197 | 198 | 199 | 200 | 201 | 202 | 203 | 204 | 205 | 206 | 207 | 208 | 209 | 210 | 211 | 212 | 213 | 214 | 215 | 216 | 217 | 218 | 219 | 220 | 221 | 222 | 223 | 224 | 225 | 226 | 227 | 228 | 229 | 230 | 231 | 232 | 233 | 234 | 235 | 236 | 237 | 238 | 239 | 240 | 241 | 242 | 243 | 244 | 245 | 246 | 247 | 248 | 249 | 250 | 251 | 252 | 253 | 254 | 255 | 256 | 257 | 258 | 259 | 260 | 261 | 262 | 263 | 264 | 265 | 266 | 267 | 268 | 269 | 270 | 271 | 272 | 273 | 274 | 275 | 276 | 277 | 278 | 279 | 280 | 281 | 282 | 283 | 284 | 285 | 286 | 287 | 288 | 289 | 290 | 291 | 292 | 293 | 294 | 295 | 296 | 297 | 298 | 299 | 300 | 301 | 302 | 303 | 304 | 305 | 306 | 307 | 308 | 309 | 310 | 311 | 312 | 313 | 314 | 315 | 316 | 317 | 318 | 319 | 320 | 321 | 322 | 323 | 324 | 325 | 326 | 327 | 328 | 329 | 330 | 331 | 332 | 333 | 334 | 335 | 336 | 337 | 338 | 339 | 340 | 341 | 342 | 343 | 344 | 345 | 346 | 347 | 348 | 349 | 350 | 351 | 352 | 353 | 354 | 355 | 356