なんつーもんを日曜日に見せてくれてんだ、三谷幸喜。
もう、月曜日からまともな精神状態で働けない・・・(´;ω;`)自分ってあまりドラマとか映画とかでうわ~って感情持ってかれない方なんだけど、今回は萎えた。絶望した。
そもそも、ガイドブックに書いてあったあらすじを読んだ時から胸糞悪かったんだけど、今後はこんな粛清が毎週続くわけで、見てて嫌になった『新選組!』の後半よりも辛いかもしれない。
基本的にはコメディタッチというギャップがある分、本当に辛い『アウトレイジビヨンド』だと思います。
片岡刑事は後白河法皇だよな。『アウトレイジビヨンド』映画館で観た時から思ったもん。「頼朝追討の院宣を出しといて、今度は義経追討だあ?てめえの舌は何枚あるんだコノヤロウ!」あ、これは池内組長か(^_^;)
さて、源頼朝ひどすぎるだろってツイッターでは阿鼻叫喚だったけど、冷静に頼朝の立場で考えてみると、ああするしかなかったよな。
不良だらけの荒れたクラスの担任になっちゃった、わりと育ちのいい教師が、今後一年間クラスをコントロールするために最初にやるのは、クラスのリーダー格を押さえつけちゃうことだからね。これに失敗すると学級崩壊待ったなしだしな。
男の子って、「オレがボスだ」って最初に見せつけちゃうと割と素直に従うからね。女子は違うと思うけど。
それに、頼朝が対峙してるのって、神奈川のヤンキーどころか首狩り族だからね。
そんな野蛮な連中、心から信じろって言っても難しいものがあるよな。慕ってくれているのはわかるけど、やっぱりめっちゃ怖いだろ。顔が怖いのよとか言ってたし。
こんな反乱がまた起きたら、今度は本当に殺されちゃうかもしれないしね。
上総広常を演じていた佐藤浩市さんが言っていたけど、最期は「あれ?オレの立ち居振る舞い間違ってたの?」って感じでやられちゃったのも、すごいリアルでよかった。
『古畑任三郎』で毎週殺人事件起こして人間を葬ってきただけあって、三谷さんって殺害シーンが妙に生々しい時あるんだよな。『真田丸』の室賀正武(黙れ小童)とか。
ボスである源頼朝に対して、みんなの前でもタメ口なのがまずかったんだよな。本人には悪意がなくても、相棒みたいな、対等な関係に風に見えるもんね。
多分、上総介のあの横柄な態度に対しては、頼朝も個人的にはそこまで気分を害していないと思うんだよ。裏で怒っているっていう描写もなかったし。この人が加勢してくれたおかげで、平家を巻き返せたわけで、恩は感じていると思うし。
でも、今後の体制づくりにどうしても非情にやるしかなかったんだっていう。「あれは謀反人だ」ってセリフは自分に言い聞かせているっていう。
上総介殿がもう少しピュアじゃなかったら、素直な男じゃなかったら、多分、みんなの前では頼朝にかしずいて、頼朝と二人きりの時だけ「武衛、飲もうぜ」とかやってたと思うんだけど、そこまで器用な人じゃなかったんだよね。
ちなみに、「かずさ」と言うと、『ときめきメモリアル2』で八重さんの声を演じた村井かずささんが思い出されるんだけど、奇しくもこのドラマの八重さんも、ときメモ2の八重さんみたいな展開で小四郎殿が攻略してて(よく2年間耐えた!)、村井かずさに縁があるドラマだなと思いました。
1100円からの再出発
2022-04-03 18:25:56 (3 years ago)
-
カテゴリタグ:
- ゲーム

お久しぶりです。最近暑かったり寒かったり、雪降ったり雨降ったり、地面揺れたり、気候が安定しないですよね。いつの間にか桜咲いてたし。
3月末にとうとうマンボウが去ったので、マイホのゲーセンで戦いを本格的に再始動しました。基本的にコロナが落ち着いている時と長期休み中は設定がいい傾向にあるんですが、2月があまりにも勝てなかったため、チキンプレイに徹しました。
あと、戦時中ということで電気代やガソリン代があまりにも高く、メダルを1万円分ポーンと買うお小遣いもないので、とりあえず3月19日に1100円払って500枚からスタートしました。
カラコロッタ5フローズンアイランド
奥さんが好きな機種の新作。主な変更点としては次の3つ。
①ワンダーチャンスが巡回ではなくまっすぐ進むようになった。
②エメラルドジャックポットチャンスが増えた。
③新ゲームが2つ増えた。
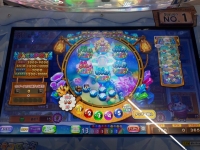
ワンダーチャンスは、150マス上に進むだけのシンプルなすごろくとなり、前と比べてジャックポットチャンスにいけるかいけないかがすごいはっきりしたので(盤面に球数増加がないとほぼ不可能)、個人的にはこっちのほうが話がわかりやすくて好き。
すべての色が1~5マス進むようにカバーされるようになったが・・・

こういう時、アウトに入ってしまったら計り知れない悔しさを味わえる。
基本的に、今回のワンダーチャンスは、手持ちの20球で150マス進むのが不可能なため、ワンダーチャンス中はスペシャルに何回かはマシンが入れてくるだろうと見越して、スペシャルの恩恵が強いトーテムやトロッコ、コロッタタワー(新ゲーム。フローズンタワーみたいなやつで結構楽しい)を選んでおくといいかも。
じゃないと、本当にワンダーチャンスは何ももらえずノーマネーでフィニッシュする。ノーマネーの場合は回収期確定なのでやめやすいけどね。
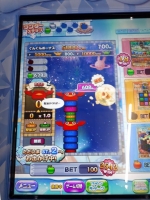

てことで、スペシャルの恩恵が強い、トーテムぐんぐん。高度634メートル(※奇しくも東京スカイツリーと同じ高さ!)という前人未到のバベルの塔を建設することができました。

初めてバブルクラップで全消し!全消しボーナスってほぼ不可能な代わりにベット数の50倍っぽいので、20枚賭けで1000枚にもなる。強い。



最初の3球でアウトに入りだしたら回収期確定なので、やめるかベット数を下げましょう。とにかく手持ちが少ない時はリンゴが何個かあるステーションをハイエナしてチキンプレー。

大事件が起きた初エメラルドジャックポットチャンス。わずか25球で最低でも4球以上内周にいかないと、ジャックポットが取れないため、絶望視していたが・・・

まさかの12倍!

おまけに次のワンダーで苦手なコイツも獲れたので、この日はカラコロッタプレー史上最大の大爆増!


別日に高額トパーズも獲れ、新台のハネムーン設定の恩恵?を受けられました!多分程なくして、えげつない回収期が来そうなので、今後はイベントで金リンゴが100円で買える火曜日しかやらないほうがいいかも・・・
総括すると、コロッタタワーがすごい楽しい。パティシエッタとか一時期狂ったようにやってたからな。スペシャルに入るとフリーゲームみたく、全ライン解放するのも熱いし。
あと名前も覚えてないくらいハマらなかった対戦仕様のスケートの新ゲームがあるんだけど、あいつはよくわからん。
グランドクロスGOLD
金土日がイベントでゴールド&シルバーJPの初期値5000枚で、上乗せ加算も5000枚カンスト状態だとえらいことになるやつ。ただし、メダルの消費量がプッシャーとは思えないくらいえげつないので、休日の朝にいい台を見つけて短期決戦すると、かなり増える。
とりあえず、19日に買ったメダル500枚を爆増させるファインプレーを見せてくれたのがこの機種で、本当に今の自分があるのもパトラさんのおかげっすわ。


超ガラポンもある程度続くとかなり強い。



ジュエルスクラッチが気持ちよく消せると、だいたいジャックポットチャンスも取れちゃったりするので、やはり奥の円盤ルーレットも内部と連動してるっぽい。









とにかく朝イチに座るとわりとポンポン1番や11番に入ってくれるので、メダルが心もとない時に本当にお世話になった。
最近は、上乗せが溜まっている台がなかなかないのと、そういうチャンス台は朝でも座られちゃうようになったので、やってないんだよな。でもここまで乱獲できたのは本当に感謝しかない。
フォーチュントリニティ3
ステーションチャレンジの操作があまりにも露骨で、精神的に余裕があるときしかプレーできないんだけど、ちょこちょこ取れました。5000枚のジャックポットで3500枚落ちるので、本当にジャックポットの爽快感はトップクラスなんだけど、通常ゲームがストレスしかないからな・・・



2倍のオーシャンは同じステーションで2夜連続で取れた。マグロ!
アニマロッタ6星の物語
ジャックポット不可能だと思う。※未だ処女です。



フィーチャープレミアム
今回は、こいつのプレーを封印したことでメダルが増えだした。最近はグラクロとカラコロッタのおかげでかなりメダルに余裕ができたので、よせばいいのに回してしまうという・・・



2月にこいつのせいで何度も破産しているので500~1000枚くらい増えたら、すぐにやめるようにしています。上のやつは珍しく跳ねたやつ。比較的にディナーの方が内部がいいことが多い。プラムの確定音スペシャルボーナスで9600枚は気持ちよかった。でも、本当にこのゲームは怖い。リセットされてる休日の朝しかやらないほうがいいな。
スマッシュスタジアム
ジャックポットチャンスで初球で終了に何度も入るなど、正直あまり楽しくはないが、ほかのゲームにお腹いっぱいになった時にちょっとだけやってます。マジで旧作に戻してくれ・・・


最近テコ入れなのか、スピンジャックポットの初期値が1000枚から1500枚になってました。確かにそれくらいしないと、割に合わないよな。
つーか、スマッシュスタジアムは、あの打たせ湯みたいな装置の払い出し位置が横穴直行なので、もっと初期値上げてもいいくらいよ。ジャックポット獲るのもかなり難しいからな。
ガッ釣りGO!
松方への道以来ほとんどやってなかったんだけど、最近仲良くなった常連のおばさんに誘われて、本日4ヶ月ぶりくらいにプレーしました。


ミニじゃない本家爆釣モードに初めて突入でき、店内ランキングで天下を取れたのですが、お魚図鑑のデータが消滅してました。有効期限あるのアレ!!???もうモチベーションが完全に絶たれた(´;ω;`)
こういうやり込み要素のデータはコンマイみたいにしっかり保存しといてほしいぜ。
てことで、3月19日~4月3日の死闘で、500枚をわらしべ長者的に65000枚にまで増やすことができました!
勝因は、フィーチャープレミアムを封印したことと、グランドクロスGOLDのファインプレーと、フローズンアイランドのダメ押しだな。
今年の目標は年末までに20万枚なので、回収期にどこまで損失を減らせるかが目標達成の鍵になりそう。まあ、数週間後に破産している気もするけど。いや、ビデスロをやらなければ多分勝てる・・・!
バレる嘘をつくしかない時代
2022-03-17 21:44:54 (3 years ago)
ロシア・ウクライナ危機、プーチン大統領の見立てが外れて、けっこう長引いている。
もともとゼレンスキー大統領って国民からの支持率が低かったから、クリミアみたいに短期決戦で電撃的にパパパっといけると思ったんだろうけど、こうなると晩年の豊臣秀吉の朝鮮出兵みたいにグダグダになってフェードアウトしそう。
プーチンさんも歳だし、判断力が衰えたって話もあるけど、そうなると定年退職がない独裁制って危険だよね。次は、習近平さんあたりも危なくなってきそう。
なんとなく、冷戦集結みたいに、ロシアが経済的に根を上げて、さらにプーチンさんも体調不良とかになって、中止みたくなるのかもな。ほいで、「これは敗北ではない、ウクライナのNATOの加盟が見送られたのだから、あの侵攻は勝利なのだ!」とか言って。
で、アメリカなんかはロシアは人殺しだとか言ってて、確かにそれはそうなんだけど、自分なんかはイラク戦争とかまだ覚えてるからな。あれだって大義名分あったのかっていう。
いや、イラクの時は独裁体制を崩して民主化しようとしたんだ、今回は独裁体制の国が民主国家を襲撃している、とか言い分はあるんだろうけど、それでもイラク戦争だって罪のない民間人がかなり亡くなったからね。
結局、PR合戦というか、情報戦なんだなって思う。その点、アメリカなんかはうまいなって思う(ロシアが下手なだけかもしれないけど)。中国への牽制の仕方とか、うまいなって。「中国がロシアを支援しているという情報がある」とかウソかホントかわからないこと言って、中国に「そんなのでっち上げだ!」って言わせてさ。あれって、中国にその言質を取るために言ってそうだもんな。
今回ショッキングなのは、ロシアもウクライナもどっちかというと先進国で、そういった国家同士が戦っているってことだよね。
なんか、中東とかアフリカとか、なんとなく貧しいイメージのあるエリアが部族紛争とかやってて、先進国は(裏で代理戦争を操れど)さすがにもう戦争なんかしないだろって、なんとなく思ってたからね。でも、豊かな国同士でもやるときゃやるんだっていう。
う~ん・・・冷戦終結時にNATOも一緒に解散してよかったんじゃないかって、ちょっと頭によぎったけど、事情があったんだろうな。
ロシアの人だって、みんながみんな賛成してないしな。すげ~嫌な仕事だって思いながら進軍しているロシア兵もたくさんいそうだし・・・
ロシアの国際的地位を著しく後退させただけの、無意味なイベントだったとか、後世の歴史の教科書で評価されそう・・・
結局、ここまで情報化が進むと、政府はなかなか嘘がつきにくくなっちゃうってことだよね。嘘まで行かなくても、なんかの情報を隠蔽するとか。リアルタイムでネットに情報がバンバンあがちゃうから、いくらでも裏が取れちゃうし。
でもさ、円滑な国家運営のために、政府が国民を欺かないといけない場面って多かれ少なかれあると思うんだよ。日本だって大いにあるじゃん。
そういう時、政府はどうすればいいのかっていう課題があるよね。今回のウクライナ危機にしろ。コロナにしろ。
やっぱりマスコミやネットコンテンツなどの洗脳ツールによるプロパガンダがキーになってくるんだろうな。オタキングは先見の明があったよ。まさか、全部つまびらか(トランスペアレンシー)にしろってことになるわきゃないし。政治が機能不全になるからな。
もともとゼレンスキー大統領って国民からの支持率が低かったから、クリミアみたいに短期決戦で電撃的にパパパっといけると思ったんだろうけど、こうなると晩年の豊臣秀吉の朝鮮出兵みたいにグダグダになってフェードアウトしそう。
プーチンさんも歳だし、判断力が衰えたって話もあるけど、そうなると定年退職がない独裁制って危険だよね。次は、習近平さんあたりも危なくなってきそう。
なんとなく、冷戦集結みたいに、ロシアが経済的に根を上げて、さらにプーチンさんも体調不良とかになって、中止みたくなるのかもな。ほいで、「これは敗北ではない、ウクライナのNATOの加盟が見送られたのだから、あの侵攻は勝利なのだ!」とか言って。
で、アメリカなんかはロシアは人殺しだとか言ってて、確かにそれはそうなんだけど、自分なんかはイラク戦争とかまだ覚えてるからな。あれだって大義名分あったのかっていう。
いや、イラクの時は独裁体制を崩して民主化しようとしたんだ、今回は独裁体制の国が民主国家を襲撃している、とか言い分はあるんだろうけど、それでもイラク戦争だって罪のない民間人がかなり亡くなったからね。
結局、PR合戦というか、情報戦なんだなって思う。その点、アメリカなんかはうまいなって思う(ロシアが下手なだけかもしれないけど)。中国への牽制の仕方とか、うまいなって。「中国がロシアを支援しているという情報がある」とかウソかホントかわからないこと言って、中国に「そんなのでっち上げだ!」って言わせてさ。あれって、中国にその言質を取るために言ってそうだもんな。
今回ショッキングなのは、ロシアもウクライナもどっちかというと先進国で、そういった国家同士が戦っているってことだよね。
なんか、中東とかアフリカとか、なんとなく貧しいイメージのあるエリアが部族紛争とかやってて、先進国は(裏で代理戦争を操れど)さすがにもう戦争なんかしないだろって、なんとなく思ってたからね。でも、豊かな国同士でもやるときゃやるんだっていう。
う~ん・・・冷戦終結時にNATOも一緒に解散してよかったんじゃないかって、ちょっと頭によぎったけど、事情があったんだろうな。
ロシアの人だって、みんながみんな賛成してないしな。すげ~嫌な仕事だって思いながら進軍しているロシア兵もたくさんいそうだし・・・
ロシアの国際的地位を著しく後退させただけの、無意味なイベントだったとか、後世の歴史の教科書で評価されそう・・・
結局、ここまで情報化が進むと、政府はなかなか嘘がつきにくくなっちゃうってことだよね。嘘まで行かなくても、なんかの情報を隠蔽するとか。リアルタイムでネットに情報がバンバンあがちゃうから、いくらでも裏が取れちゃうし。
でもさ、円滑な国家運営のために、政府が国民を欺かないといけない場面って多かれ少なかれあると思うんだよ。日本だって大いにあるじゃん。
そういう時、政府はどうすればいいのかっていう課題があるよね。今回のウクライナ危機にしろ。コロナにしろ。
やっぱりマスコミやネットコンテンツなどの洗脳ツールによるプロパガンダがキーになってくるんだろうな。オタキングは先見の明があったよ。まさか、全部つまびらか(トランスペアレンシー)にしろってことになるわきゃないし。政治が機能不全になるからな。
バースデーカウンター寿司
2022-03-05 21:41:23 (3 years ago)
-
カテゴリタグ:
- 雑記
38になりました。もう30代が終わるというのか・・・!!信じぬ・・・!!!
それで、奥さんがなんでも美味しいものをご馳走してくれるというので、直前にがっぽり寿司で遊んだことだし、「お寿司が食べたい」とおねだりしたんだけど、チェーン店の回転寿司がどこもファミリーでごった返していて、そのうえマンボウの時短営業のせいで8時には閉まっているところも多く、空腹状態のままさまよっていたんですが、偶然路地裏の中に明かりがついている寿司屋を発見し突撃したら、そこがとんでもない高級店で、久しぶりに本当に美味しいものをいただきました。
自分の財布には7千円しか入っておらず、奥さんのキャッシュが頼りだったんですが、奥さんは現金主義者なのでニコニコ現金払い。本当にごちそうさまでした。プレゼントとケーキもありがとうございます。
つーか、太刀魚とか人生で初めて食べたよ。アウトレイジ3に出てくる伝説の高級魚という知識しかなかったし。あと、ハマチって高級店では出さないのね。ブリならともかく、ハマチは格下なんだって・・・
ちなみに今年は自分の運気は最高らしいだけど、メダルゲームでは勝てねえわ、おばあちゃんも亡くなるわ、コロナ終わらねえわ、戦争始まるわで、本当に運気がいいのかって思ってたけど、とうとうハッピーなイベントが来たよ。
ネギトロも美味かったな~・・・高級店のネギトロってあんな感じになるのか。軍艦じゃないのね。
それで、奥さんがなんでも美味しいものをご馳走してくれるというので、直前にがっぽり寿司で遊んだことだし、「お寿司が食べたい」とおねだりしたんだけど、チェーン店の回転寿司がどこもファミリーでごった返していて、そのうえマンボウの時短営業のせいで8時には閉まっているところも多く、空腹状態のままさまよっていたんですが、偶然路地裏の中に明かりがついている寿司屋を発見し突撃したら、そこがとんでもない高級店で、久しぶりに本当に美味しいものをいただきました。
自分の財布には7千円しか入っておらず、奥さんのキャッシュが頼りだったんですが、奥さんは現金主義者なのでニコニコ現金払い。本当にごちそうさまでした。プレゼントとケーキもありがとうございます。
つーか、太刀魚とか人生で初めて食べたよ。アウトレイジ3に出てくる伝説の高級魚という知識しかなかったし。あと、ハマチって高級店では出さないのね。ブリならともかく、ハマチは格下なんだって・・・
ちなみに今年は自分の運気は最高らしいだけど、メダルゲームでは勝てねえわ、おばあちゃんも亡くなるわ、コロナ終わらねえわ、戦争始まるわで、本当に運気がいいのかって思ってたけど、とうとうハッピーなイベントが来たよ。
ネギトロも美味かったな~・・・高級店のネギトロってあんな感じになるのか。軍艦じゃないのね。
進撃のプーチン
2022-02-27 11:44:29 (3 years ago)
-
カテゴリタグ:
- 雑記
松屋が改修工事で久しぶりに珈琲館で朝食を取ったんだけど、そこで読んだ新聞に今回のウクライナ侵攻のことがかなり紙面を割いて書かれていました。
とりあえず、千葉常胤じゃないけど、齢60を過ぎてお迎えを待つだけと思っていたら、人生最後の戦のチャンスが来たって感じなのだろうか。
めちゃくちゃ迷惑だけど、ロシアの歴史において、クリミア半島あたりの温暖なエリアの獲得は悲願って感じがするから、今に始まったことではないんだよな。
今回のウクライナの話だって、今年に突然とかじゃないじゃん。2014年のクリミアのロシア編入あたりからもうきな臭いし。あれでロシアはG8からはぶられちゃったしね。
というかウクライナってでかいんだよね。日本よりもでかいし、土壌はチェルノーゼムで肥沃だから、農作物もたくさん生産できるし。アルザスロレーヌとか、シュレジエンみたいに美味しいエリアなのだろう。
で、こういう地政学的な争奪戦はもうやめようってことでEUとか地域的経済連携ができたわけだから、ロシアも冷戦終わったらすぐに、EUに混ぜちゃえばよかったんだよな。まあ、EUはイギリスですら抵抗があったわけだから難しかったんだろうけど。
もっと言えば、冷戦が終わったら、NATOもWTOも一旦解散させて、新しい合同軍事チームを再編成すればよかったんだよな。新NATOみたいな。
そういうグループに欧米露をまとめちゃえば、今回みたいなことにはならなかったのかもしれないけど、これも欧米の方がむしろ抵抗しそうだし、実現できても国連の安全保障理事会みたいに決裂するかもしれない。
で、プーチンさんなんだけど、この人はもう生粋の武闘派じゃないですか。平和ボケした日本人の常識じゃ想像も及ばない戦闘民族だから。
暗殺されちゃった可能性があるアンナ・ポリトコフスカヤさんの『プーチニズム』を漫画の取材で読んだことがあるんだけど、ノルドオスト事件とかドン引きだもん。
やっぱりロシアの人(特に下層の人)ってマッチョイズムというか、強いリーダーに惹かれるところがあるみたくて。ケンカが強いヤツがモテるみたいな。
で、振り返れば、プーチンさんって頭角を現したチェチェン紛争から負け知らずというか、戦が上手じゃん。
今回のウクライナ侵攻だって、絶対に勝算があって実行しているはずだから、おそらく現政権のゼレンスキーさんは気の毒だけど追い払われて、親露政権が樹立される気がする。
ただし、圧倒的な大部隊を送り込めばクリミアみたいに無血開城できるだろという見通しだけは外れて、今回はウクライナがかなり抵抗しているから、ちょっと手こずっているそうなんだけね。
とはいえ、欧米が本格的に軍事介入してくることはないっていう見通しがプーチンさんの中にはあるのだろう。
実際にバイデンさんも、ここで全面対決したらポーランドとかドイツとかフランスとか陸続きのNATO加盟国も戦火に包まれちゃう可能性があるから、経済制裁と和平交渉でなんとか済ませたいんだと思うけど、それでプーチンさんが引き下がるわけないと思うんだよな。多分、今回の戦もプーチンが勝つと思う。外れて欲しいけど。
で、そうなってしまうと、日本はもう人事じゃないんだよ。ネット上では嘲笑されがちなネトウヨが言っていた、中国の驚異が現実味を帯びるというか。
このパワープレイでいけるんだっていう前例を作ってしまうと、今回ロシアの後ろ盾をしていると思われる中国が、じゃあ、台湾も尖閣も沖縄も、ごり押しで乗っ取れるんじゃないかって自信をつけちゃうんだよな。
なんだかんだ言って、欧米は武力制裁はしないぞっていう。いける、いけるっていう。
これは、本当にやってくれたなプーチンだよね。
考えれば、日本って位置的に周囲が北朝鮮、韓国、中国、ロシアってヤバイ国ばっかりで、そうなるといよいよ憲法9条改正も考えなきゃいけなくなるのかもしれない。自国は自分で防衛しなきゃいけないってことだから(よく考えてみれば当たり前なんだけど)。
だから、桜を見る会とか色々あったけど、皮肉にも安倍さんみたいな外交や地政学に強い総理大臣がまた必要になってくるんじゃないか。反安倍の人とか、今回はどう思っているんだろう。
安倍が総理になるくらいなら、尖閣諸島くらい朝貢しちゃえって感じなのかなあ。
むしろ、今の岸田政権って中国と近いから、それを逆手にとって欧米を脅すとか?おい、ちゃんと日本を中国から守ってくれないと、日本は中国の冊封体制につくぞ、みたいな。
これはアメリカは結構焦ると思うけどな。でも、万が一どうぞどうぞってなると、日本から選挙制度はなくなり、中国の息のかかった政治家が総理大臣として出向してくるに違いない。
とりあえず、千葉常胤じゃないけど、齢60を過ぎてお迎えを待つだけと思っていたら、人生最後の戦のチャンスが来たって感じなのだろうか。
めちゃくちゃ迷惑だけど、ロシアの歴史において、クリミア半島あたりの温暖なエリアの獲得は悲願って感じがするから、今に始まったことではないんだよな。
今回のウクライナの話だって、今年に突然とかじゃないじゃん。2014年のクリミアのロシア編入あたりからもうきな臭いし。あれでロシアはG8からはぶられちゃったしね。
というかウクライナってでかいんだよね。日本よりもでかいし、土壌はチェルノーゼムで肥沃だから、農作物もたくさん生産できるし。アルザスロレーヌとか、シュレジエンみたいに美味しいエリアなのだろう。
で、こういう地政学的な争奪戦はもうやめようってことでEUとか地域的経済連携ができたわけだから、ロシアも冷戦終わったらすぐに、EUに混ぜちゃえばよかったんだよな。まあ、EUはイギリスですら抵抗があったわけだから難しかったんだろうけど。
もっと言えば、冷戦が終わったら、NATOもWTOも一旦解散させて、新しい合同軍事チームを再編成すればよかったんだよな。新NATOみたいな。
そういうグループに欧米露をまとめちゃえば、今回みたいなことにはならなかったのかもしれないけど、これも欧米の方がむしろ抵抗しそうだし、実現できても国連の安全保障理事会みたいに決裂するかもしれない。
で、プーチンさんなんだけど、この人はもう生粋の武闘派じゃないですか。平和ボケした日本人の常識じゃ想像も及ばない戦闘民族だから。
暗殺されちゃった可能性があるアンナ・ポリトコフスカヤさんの『プーチニズム』を漫画の取材で読んだことがあるんだけど、ノルドオスト事件とかドン引きだもん。
やっぱりロシアの人(特に下層の人)ってマッチョイズムというか、強いリーダーに惹かれるところがあるみたくて。ケンカが強いヤツがモテるみたいな。
で、振り返れば、プーチンさんって頭角を現したチェチェン紛争から負け知らずというか、戦が上手じゃん。
今回のウクライナ侵攻だって、絶対に勝算があって実行しているはずだから、おそらく現政権のゼレンスキーさんは気の毒だけど追い払われて、親露政権が樹立される気がする。
ただし、圧倒的な大部隊を送り込めばクリミアみたいに無血開城できるだろという見通しだけは外れて、今回はウクライナがかなり抵抗しているから、ちょっと手こずっているそうなんだけね。
とはいえ、欧米が本格的に軍事介入してくることはないっていう見通しがプーチンさんの中にはあるのだろう。
実際にバイデンさんも、ここで全面対決したらポーランドとかドイツとかフランスとか陸続きのNATO加盟国も戦火に包まれちゃう可能性があるから、経済制裁と和平交渉でなんとか済ませたいんだと思うけど、それでプーチンさんが引き下がるわけないと思うんだよな。多分、今回の戦もプーチンが勝つと思う。外れて欲しいけど。
で、そうなってしまうと、日本はもう人事じゃないんだよ。ネット上では嘲笑されがちなネトウヨが言っていた、中国の驚異が現実味を帯びるというか。
このパワープレイでいけるんだっていう前例を作ってしまうと、今回ロシアの後ろ盾をしていると思われる中国が、じゃあ、台湾も尖閣も沖縄も、ごり押しで乗っ取れるんじゃないかって自信をつけちゃうんだよな。
なんだかんだ言って、欧米は武力制裁はしないぞっていう。いける、いけるっていう。
これは、本当にやってくれたなプーチンだよね。
考えれば、日本って位置的に周囲が北朝鮮、韓国、中国、ロシアってヤバイ国ばっかりで、そうなるといよいよ憲法9条改正も考えなきゃいけなくなるのかもしれない。自国は自分で防衛しなきゃいけないってことだから(よく考えてみれば当たり前なんだけど)。
だから、桜を見る会とか色々あったけど、皮肉にも安倍さんみたいな外交や地政学に強い総理大臣がまた必要になってくるんじゃないか。反安倍の人とか、今回はどう思っているんだろう。
安倍が総理になるくらいなら、尖閣諸島くらい朝貢しちゃえって感じなのかなあ。
むしろ、今の岸田政権って中国と近いから、それを逆手にとって欧米を脅すとか?おい、ちゃんと日本を中国から守ってくれないと、日本は中国の冊封体制につくぞ、みたいな。
これはアメリカは結構焦ると思うけどな。でも、万が一どうぞどうぞってなると、日本から選挙制度はなくなり、中国の息のかかった政治家が総理大臣として出向してくるに違いない。
- Calendar
<< January 2026 >> Sun Mon Tue Wed Thu Fri Sat 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
- search this site.
- tags
-
- 漫画 (387)
- 脚本 (243)
- 映画 (235)
- 雑記 (163)
- ゲーム (156)
- 本 (116)
- 教育 (107)
- 生物学 (105)
- 科学 (93)
- 社会学 (81)
- 歴史 (72)
- テレビ (71)
- 芸術 (61)
- 政治 (50)
- 数学 (40)
- 進化論 (40)
- 資格試験 (38)
- 情報 (38)
- サイト・ブログ (37)
- 語学 (37)
- 映画論 (36)
- 物理学 (33)
- 哲学 (32)
- 恐竜 (29)
- 育児 (28)
- 文学 (26)
- 化学 (25)
- 論文 (22)
- PIXAR (22)
- 心理学 (18)
- 地学 (16)
- 気象学 (15)
- 地理学 (15)
- 技術 (13)
- 経済学 (12)
- 医学 (11)
- 玩具 (9)
- 司書 (8)
- 法律学 (7)
- 対談 (5)
- スポーツ (4)
- 映画の評価について (1)
- プロフィール (1)
- archives
-
- 202601 (2)
- 202512 (4)
- 202511 (15)
- 202510 (8)
- 202509 (5)
- 202508 (3)
- 202507 (3)
- 202506 (3)
- 202505 (1)
- 202504 (2)
- 202503 (2)
- 202502 (2)
- 202501 (1)
- 202412 (2)
- 202411 (6)
- 202410 (2)
- 202409 (4)
- 202408 (4)
- 202407 (7)
- 202406 (27)
- 202405 (11)
- 202404 (4)
- 202403 (23)
- 202402 (22)
- 202401 (15)
- 202312 (4)
- 202311 (7)
- 202310 (2)
- 202309 (8)
- 202308 (9)
- 202307 (8)
- 202306 (5)
- 202305 (15)
- 202304 (4)
- 202303 (4)
- 202302 (2)
- 202301 (4)
- 202212 (15)
- 202211 (7)
- 202210 (5)
- 202209 (4)
- 202208 (4)
- 202207 (7)
- 202206 (2)
- 202205 (5)
- 202204 (3)
- 202203 (2)
- 202202 (5)
- 202201 (6)
- 202112 (6)
- 202111 (4)
- 202110 (6)
- 202109 (7)
- 202108 (5)
- 202107 (8)
- 202106 (4)
- 202105 (8)
- 202104 (4)
- 202103 (6)
- 202102 (10)
- 202101 (3)
- 202012 (12)
- 202011 (3)
- 202010 (4)
- 202009 (5)
- 202008 (6)
- 202007 (4)
- 202006 (4)
- 202005 (4)
- 202004 (7)
- 202003 (5)
- 202002 (6)
- 202001 (8)
- 201912 (6)
- 201911 (5)
- 201910 (3)
- 201909 (4)
- 201908 (10)
- 201907 (3)
- 201906 (6)
- 201905 (10)
- 201904 (3)
- 201903 (7)
- 201902 (8)
- 201901 (5)
- 201812 (7)
- 201811 (12)
- 201810 (7)
- 201809 (5)
- 201808 (10)
- 201807 (5)
- 201806 (19)
- 201805 (14)
- 201804 (11)
- 201803 (15)
- 201802 (4)
- 201801 (6)
- 201712 (4)
- 201711 (3)
- 201710 (11)
- 201709 (9)
- 201708 (15)
- 201707 (7)
- 201706 (4)
- 201705 (5)
- 201704 (6)
- 201703 (7)
- 201702 (6)
- 201701 (3)
- 201612 (3)
- 201611 (7)
- 201610 (7)
- 201609 (2)
- 201608 (8)
- 201607 (8)
- 201606 (7)
- 201605 (3)
- 201604 (4)
- 201603 (8)
- 201602 (3)
- 201601 (2)
- 201512 (3)
- 201511 (3)
- 201510 (4)
- 201509 (4)
- 201508 (8)
- 201507 (17)
- 201506 (2)
- 201505 (5)
- 201504 (9)
- 201503 (20)
- 201502 (7)
- 201501 (4)
- 201412 (5)
- 201411 (3)
- 201410 (2)
- 201409 (3)
- 201408 (3)
- 201407 (3)
- 201406 (12)
- 201405 (6)
- 201404 (7)
- 201403 (5)
- 201402 (12)
- 201401 (9)
- 201312 (6)
- 201311 (9)
- 201310 (8)
- 201309 (6)
- 201308 (6)
- 201307 (6)
- 201306 (10)
- 201305 (10)
- 201304 (23)
- 201303 (17)
- 201302 (16)
- 201301 (5)
- 201212 (10)
- 201211 (4)
- 201210 (18)
- 201209 (4)
- 201208 (30)
- 201207 (7)
- 201206 (4)
- 201205 (6)
- 201204 (4)
- 201203 (4)
- 201202 (3)
- 201201 (3)
- 201112 (4)
- 201111 (7)
- 201110 (3)
- 201109 (9)
- 201108 (3)
- 201107 (7)
- 201106 (2)
- 201105 (11)
- 201104 (7)
- 201103 (14)
- 201102 (19)
- 201101 (27)
- 201012 (25)
- 201011 (70)
- 201010 (34)
- 201009 (30)
- 201008 (42)
- 201007 (44)
- 201006 (29)
- 201005 (37)
- 201004 (50)
- 201003 (44)
- 201002 (48)
- 201001 (38)
- 200912 (20)
- recent trackback
- others
-
- RSS2.0
- hosted by チカッパ!
- HEAVEN INSITE(本サイト)


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 | 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 | 121 | 122 | 123 | 124 | 125 | 126 | 127 | 128 | 129 | 130 | 131 | 132 | 133 | 134 | 135 | 136 | 137 | 138 | 139 | 140 | 141 | 142 | 143 | 144 | 145 | 146 | 147 | 148 | 149 | 150 | 151 | 152 | 153 | 154 | 155 | 156 | 157 | 158 | 159 | 160 | 161 | 162 | 163 | 164 | 165 | 166 | 167 | 168 | 169 | 170 | 171 | 172 | 173 | 174 | 175 | 176 | 177 | 178 | 179 | 180 | 181 | 182 | 183 | 184 | 185 | 186 | 187 | 188 | 189 | 190 | 191 | 192 | 193 | 194 | 195 | 196 | 197 | 198 | 199 | 200 | 201 | 202 | 203 | 204 | 205 | 206 | 207 | 208 | 209 | 210 | 211 | 212 | 213 | 214 | 215 | 216 | 217 | 218 | 219 | 220 | 221 | 222 | 223 | 224 | 225 | 226 | 227 | 228 | 229 | 230 | 231 | 232 | 233 | 234 | 235 | 236 | 237 | 238 | 239 | 240 | 241 | 242 | 243 | 244 | 245 | 246 | 247 | 248 | 249 | 250 | 251 | 252 | 253 | 254 | 255 | 256 | 257 | 258 | 259 | 260 | 261 | 262 | 263 | 264 | 265 | 266 | 267 | 268 | 269 | 270 | 271 | 272 | 273 | 274 | 275 | 276 | 277 | 278 | 279 | 280 | 281 | 282 | 283 | 284 | 285 | 286 | 287 | 288 | 289 | 290 | 291 | 292 | 293 | 294 | 295 | 296 | 297 | 298 | 299 | 300 | 301 | 302 | 303 | 304 | 305 | 306 | 307 | 308 | 309 | 310 | 311 | 312 | 313 | 314 | 315 | 316 | 317 | 318 | 319 | 320 | 321 | 322 | 323 | 324 | 325 | 326 | 327 | 328 | 329 | 330 | 331 | 332 | 333 | 334 | 335 | 336 | 337 | 338 | 339 | 340 | 341 | 342 | 343 | 344 | 345 | 346 | 347 | 348 | 349 | 350 | 351 | 352 | 353 | 354 | 355 | 356