「面白い度☆☆☆☆ 好き度☆☆☆☆ 絶望感☆☆☆☆☆」
民衆が政治にうんざりして、諦めた時、独裁者は現れる。
あの『華氏911』から14年、ブッシュ大統領という強敵(とも)を失い、最近落ち着いてしまった感があったムーア監督が再び修羅の国(故郷フリント)に帰ってきた!
今度の敵は、もちろんトランプ大統領・・・!!ではなかった!(ここが一番意外だった)
オルトライトも、共和党保守派も、民主党中道派も、まとめてトランプ以上のプロパガンダ的手法で叩き潰す!
こういう題材の場合、日本だったら有権者が選挙にいかないのが悪いという、自己責任論で片付けがちなんだけど、ムーア監督は、そういったアメリカに1億人もいる政治的アパシー層を責めたりはしない。
むしろ、そりゃあ投票する気失せるよ、と民主党代表選のめちゃくちゃさを描きながら(有権者はヒラリーよりもサンダースを選んでいた!)、じゃあ投票が無意味なら、自分自身が立候補すればいいじゃないと、多数派のリベラル層に希望を与える・・・とかいうと、楽観しているような気がするけど、決してそんなことはない。
この映画の作風は過去最高に切実としていて、なんかけっこう見ていて辛いものがあったよ。
だいたい、沖縄基地問題なんかも、あれ、沖縄県民の人、アメリカの民主党支持者と同じような無力感を抱いてるんじゃないのかな。
結局沖縄県の民意は無視して、政府が統治行為論だかしらねーけど、基地建設をごり押ししてるわけじゃん。なんだよ、なんのための選挙だよバカヤローと。やる意味ねーよ、と。
国民が政府を支配しなければ、政府が国民を支配する。(報道ステーションのインタビューより)
しかし、フリントの街の惨状は・・・本当にマジか、の一言だよな・・・最近『北斗の拳』読み直してるけど、現実で、しかもアメリカという先進国で、あんな住民毒殺行為が自治体ぐるみで行われているってちょっと恐ろしいものがあるよ。そういう公害の知識がなくてやってしまった、とかじゃないからね。
この監督の映画を見てると、資本主義とモラルって両立できないのかよって感じがするけど、でもまあ、東京電力なんかも工場萌えとかなんとかいって世間の顰蹙買っちゃったし、まあ、あれは未曾有の自然現象で破壊されちゃったっていう面はあるんだけど、やっぱり、特権階級の政治家や資本家は、動かしている対象がマクロ過ぎて、感覚が麻痺しちゃうっていうのはあるんだろうな。
あの市街地での軍事演習は、絶対うるさい住民(こざかしい黒人ども)への見せしめでやったよな。
日本だと逆に、モラル警察がうるさいくらいだから、いくらなんでもここまでの横暴はできないだろ・・・とか思いがちだけど、わりとモラル警察って文句を言えれば満足なところあって、その問題を叩くのに飽きちゃったら、問題の本質的な解決には特に尽力しないからな。
表面上、上の人が謝って、みんなが問題を忘れるまで耐えてしまえばいいって思ってたりするんだろうね。
原発問題に関して言えば、国の圧力で放射能汚染の数値を、この映画みたいに改ざんされてない事を願うよ。
でも、ちょっと、アメリカってこういう映画を撮ってくれる人とかいて、羨ましいよなって思うよね。自分の信じる哲学や信念を下に自由に活動している人って、日本はあまりいないじゃん。同調しちゃうからね。日本人ってアウトローを応援しないからな。
むしろ、ホリエモンとか前澤社長とか、子どもっぽい欲望しか持っていないような幼児性のある金持ちにシンパシーを感じているところがあって情けなくはなるけどね。
武器は?
マイケル・ムーアがいる。
学校経営と学校図書館覚え書き
2018-11-03 10:35:20 (7 years ago)
-
カテゴリタグ:
- 司書
学校図書館の経営
図書館の資料やサービスを積極的に利用し、さらにそれを活用する力の育成は、文科省が提案する生きる力や、主体的・対話的で深い学びに大いに貢献するものである。
しかし、経営の観点からいえば、校務分掌で図書委員会の担当になっている先生(特に国語科教師が多い)と、生徒のみが図書室の運営に関わり、開館時間も昼休みだけに留まっているというのが現状である。
また、学校の規模によっては、学校図書館の専門家である司書教諭がそもそも配置されていないこともある。
これを踏まえて、予算など現実的な問題もあるが、学校図書館の理想的な経営を提案していきたい。
まず、経営で最も重要な点は、利用者の獲得である。
つまり、図書室に来てもらわないことには始まらないので、利用時間を増やす。昼休みだけではなく、放課後(特に部活休養日や、部活が中止となるテスト期間)や休日、長期休み期間も解放する。
そのためには、図書室の運営を図書委員会の先生だけに任せず、例えば管理当番の先生がその日の図書室の運営も行うというように、持ち回りにする。
休日や放課後の図書館営業に関しては、部活との兼ね合いがあるので、例えば読書部という部活を作り、その顧問の先生に運営させるとか、体育館や音楽室の夜間開放のように地域の人をボランティアとして手伝っていただくことも考えられる。
ふたつめに、生徒が図書館に足を運びたくなるようなサービスの充実である。
例えば、図書室の内観について書店を参考にする。本の並べ方やポップなど、プロは実際に客に本を買ってもらうためのたくさんの工夫があるので、図書委員会で書店を取材する。
次に、予算内で購入する書籍の精選である。現在公開中、もしくは近年公開した映画の原作や、国語の教科書で単元として取り上げられている作家の他の著作、テストで良く出題される作家の著作、各先生方におすすめの一冊をそれぞれ選んでもらうなど、企画を意識した購入計画を行う。
さらに、これは管理職の判断にもよるが、廃棄図書はカートに入れて欲しい生徒にあげてしまう(特に雑誌など)。もしくは文化祭のバザーなどでまとめて売ってしまう。このときの売り上げを図書館経営のための費用に充てる(実際そういうことをやっている学校があった)。
こういった限られた人材と予算の中でやれることを少しずつ実現していく。
司書教諭に求められる資質・能力
司書教諭が果たすべき役割について論じるために、まずは現在の学校教育の現状と問題点についてまとめたい。
学校図書館を使った授業の一般的イメージは、今なお、教師不在時の自習や、総合の時間での簡単な調べ学習(テキストでは「写し学習」に過ぎないと批判している)に留まっており、教師の側がまず、学校図書館をどのように活用すべきかがよく分かっていないことが大きな課題である。
この原因は、学校図書館のプロである司書教諭や学校司書の配備と配慮(時数軽減など)があまりに不十分であるからである。
この現状と課題を受けて、司書教諭に求められる能力を考えていきたい。
ひとつめは、プロモ-ション能力である。
司書教諭は、学校内で教諭や児童生徒に対して、図書館活用教育を推進する積極的な啓蒙活動を行わなければならない。
ふたつめは、問題の分析能力である。
司書教諭は、時に個々の教育活動の問題点を指摘し、改善をともに考えるという指導的・助言的役割を果たさなければならない。
みっつめは、組織内での地位と、教員としての経験にもとづく、組織の調整能力である。
図書館教育を推進するためには、図書館利用時間確保のために時間割の調整など、教育理念の策定や教育課程の企画立案に深く関わる必要があるため、司書教諭には教務主任レベルの権限や経験が求められる。
しかし、これは、若い教師が図書館運営に関わってはならないというわけではない。例えば、学校図書館のサービスを向上するために、学年と学校図書館をつなぐ橋渡し役になれば、校内の教師の学校図書館についての理解が深まり、協力体制を強化することにつながる。
よっつめは、情報発信のためのスキル(文書やホームページ作成など)である。
保護者や地域社会に対して、自分の勤務校の図書室がどういった取り組みをしているか、どんな資料があるかを図書館だよりやインターネットで発信したり(ホームページを作って収蔵している資料のデータベースを公開するとさらによい)、休日は地域に開放したりするなどして、学校図書館を広く利用してもらい、それと同時に、利用者にアンケートをとるなど、小まめにニーズを吸い上げれば、校内の職員も学校図書館の必要性や利用の仕方についての理解が深まるだろう。
最後に、司書教諭の職務は民主主義教育の根幹に関わるものであることを自覚し、自らの置かれた環境に甘えることなく、日々の仕事に着実に取り組む熱血教師的な姿勢もまた、司書教諭に求められる重要な能力である。
学校図書館における情報サービス
学校図書館のサービスは、大きく直接サービスと間接サービスに分けられる。
前者は、児童生徒や教職員にメディアや情報などを直接提供したり援助したりする諸活動のことである。
後者は、直接サービスに必要なメディアや情報を収集・整理したり、館内の環境を整備したりする諸活動のことである。
児童生徒への直接サービスには以下のものが挙げられる。
①メディア提供サービス
学校図書館が所蔵している各種のメディアを児童生徒に提供する諸活動のこと。
閲覧、貸し出し、予約・リクエストの受付などがある。
ちなみに閲覧とは、学校図書館における最も基本的な行動で、学校図書館内で読み物を読んだり、視聴覚メディアを視聴したり、インターネット接続端末を利用したりと、所蔵メディアを学校図書館内で利用すること全般を意味している。
②情報提供サービス
児童生徒が求める情報にたどりつけるように司書教諭や学校司書が援助する諸活動のことで、レファレンスサービス、レフェラルサービス、読書相談などがある。
レファレンスサービスとは、メディアの探し方がわからない、あるテーマについてどんな文献があるのか知りたいなどの情報ニーズをもつ児童生徒からのさまざまな質問や相談に対して、司書教諭や学校司書が学校図書館内の各種メディアや情報源を利用、参照して、具体的に求められた情報が記載されている箇所を提示しながら、解決できるように援助していく活動のことである。
レフェラルサービスとは、学校図書館だけでは解決が難しい質問や相談に対して、その分野の専門家や専門機関に照会して情報を入手して、あるいは専門家や専門機関を児童生徒に直接紹介して、解決できるように援助していく活動のことである。一般にレファレンスサービスの延長として行われる。
読書相談とは、児童生徒からの読書に関する質問や相談に応じるサービスのことであり、主には、読み物の選択、探索、入手の援助が中心となる。レファレンスサービスに含める考え方もある。
③図書館利用促進サービス
児童生徒に学校図書館をもっと利用してもらうように働きかける諸活動のことであり、集会(読書会、読み聞かせ会など)、行事(読書週間、読書感想文コンクールなど)、広報(図書館だより、校内放送など)、指導(利用指導、読書指導など)などがある。これらが年間を通して計画的に行われることが望ましい。
④特別な支援が必要な児童生徒に対するサービス
上述したサービスを、特別な支援が必要とする児童生徒にも等しく提供するため、独自のメディアや独自のサービスを別途用意すること。
点字図書館と連携したり、ボランティアを組織したり、館内のバリアフリー化を促進するなど。
次に、教職員へのサービスには以下のものがある。
①教育活動、授業展開に必要な資料・情報の収集と提供
授業の準備や授業展開に必要となる資料や情報を収集・提供し、教師を援助すること。
学校図書館資料の充実はもちろん、校内で分散している資料や教材の管理・把握や、優れた授業実践の記録や教材を保存し、積極的に周知、提供していくことも大切である。
また、同一地域にある他の学校図書館や公共図書館との連携や、学習支援センターの設置、さらに、教師と資料、さらには児童生徒と資料を結びつけるために、授業計画に関するアドバイスや、ティーム・ティーチングへの協力も重要な活動である。
②生活指導に必要な資料・情報の収集と提供
児童生徒の生活実態、生活の背景にあるコミュニティを理解するために役立つ資料を収集、教師に提供する。
具体的には、今日の教育問題や社会問題、地域に関する資料や情報など。
③進路指導に必要な資料・情報の収集と提供
進学・就職などに役立つ資料を収集し、提供する。
具体的には、進学先の学校の案内やシラバス、就職に関しては地域の企業、学校の特色に即した企業の要覧、説明会の資料など。
④教師の研究活動に必要な資料・情報の収集と提供
授業の教材研究や、教師個人の専門分野を伸ばすための調査や研究に必要な資料や情報を収集し、提供する。必要に応じて、大学など高等教育機関から資料を入手することもある。
⑤学校経営に必要な資料・情報の収集と提供
校務分掌や教育課程の編成、研修、教育行政などに関する資料や情報を収集し、提供する。
サービスの実施には、司書教諭だけではなく、他の教員、校長や教頭、学校事務職員と密接な連携を図る必要がある。
図書館の資料やサービスを積極的に利用し、さらにそれを活用する力の育成は、文科省が提案する生きる力や、主体的・対話的で深い学びに大いに貢献するものである。
しかし、経営の観点からいえば、校務分掌で図書委員会の担当になっている先生(特に国語科教師が多い)と、生徒のみが図書室の運営に関わり、開館時間も昼休みだけに留まっているというのが現状である。
また、学校の規模によっては、学校図書館の専門家である司書教諭がそもそも配置されていないこともある。
これを踏まえて、予算など現実的な問題もあるが、学校図書館の理想的な経営を提案していきたい。
まず、経営で最も重要な点は、利用者の獲得である。
つまり、図書室に来てもらわないことには始まらないので、利用時間を増やす。昼休みだけではなく、放課後(特に部活休養日や、部活が中止となるテスト期間)や休日、長期休み期間も解放する。
そのためには、図書室の運営を図書委員会の先生だけに任せず、例えば管理当番の先生がその日の図書室の運営も行うというように、持ち回りにする。
休日や放課後の図書館営業に関しては、部活との兼ね合いがあるので、例えば読書部という部活を作り、その顧問の先生に運営させるとか、体育館や音楽室の夜間開放のように地域の人をボランティアとして手伝っていただくことも考えられる。
ふたつめに、生徒が図書館に足を運びたくなるようなサービスの充実である。
例えば、図書室の内観について書店を参考にする。本の並べ方やポップなど、プロは実際に客に本を買ってもらうためのたくさんの工夫があるので、図書委員会で書店を取材する。
次に、予算内で購入する書籍の精選である。現在公開中、もしくは近年公開した映画の原作や、国語の教科書で単元として取り上げられている作家の他の著作、テストで良く出題される作家の著作、各先生方におすすめの一冊をそれぞれ選んでもらうなど、企画を意識した購入計画を行う。
さらに、これは管理職の判断にもよるが、廃棄図書はカートに入れて欲しい生徒にあげてしまう(特に雑誌など)。もしくは文化祭のバザーなどでまとめて売ってしまう。このときの売り上げを図書館経営のための費用に充てる(実際そういうことをやっている学校があった)。
こういった限られた人材と予算の中でやれることを少しずつ実現していく。
司書教諭に求められる資質・能力
司書教諭が果たすべき役割について論じるために、まずは現在の学校教育の現状と問題点についてまとめたい。
学校図書館を使った授業の一般的イメージは、今なお、教師不在時の自習や、総合の時間での簡単な調べ学習(テキストでは「写し学習」に過ぎないと批判している)に留まっており、教師の側がまず、学校図書館をどのように活用すべきかがよく分かっていないことが大きな課題である。
この原因は、学校図書館のプロである司書教諭や学校司書の配備と配慮(時数軽減など)があまりに不十分であるからである。
この現状と課題を受けて、司書教諭に求められる能力を考えていきたい。
ひとつめは、プロモ-ション能力である。
司書教諭は、学校内で教諭や児童生徒に対して、図書館活用教育を推進する積極的な啓蒙活動を行わなければならない。
ふたつめは、問題の分析能力である。
司書教諭は、時に個々の教育活動の問題点を指摘し、改善をともに考えるという指導的・助言的役割を果たさなければならない。
みっつめは、組織内での地位と、教員としての経験にもとづく、組織の調整能力である。
図書館教育を推進するためには、図書館利用時間確保のために時間割の調整など、教育理念の策定や教育課程の企画立案に深く関わる必要があるため、司書教諭には教務主任レベルの権限や経験が求められる。
しかし、これは、若い教師が図書館運営に関わってはならないというわけではない。例えば、学校図書館のサービスを向上するために、学年と学校図書館をつなぐ橋渡し役になれば、校内の教師の学校図書館についての理解が深まり、協力体制を強化することにつながる。
よっつめは、情報発信のためのスキル(文書やホームページ作成など)である。
保護者や地域社会に対して、自分の勤務校の図書室がどういった取り組みをしているか、どんな資料があるかを図書館だよりやインターネットで発信したり(ホームページを作って収蔵している資料のデータベースを公開するとさらによい)、休日は地域に開放したりするなどして、学校図書館を広く利用してもらい、それと同時に、利用者にアンケートをとるなど、小まめにニーズを吸い上げれば、校内の職員も学校図書館の必要性や利用の仕方についての理解が深まるだろう。
最後に、司書教諭の職務は民主主義教育の根幹に関わるものであることを自覚し、自らの置かれた環境に甘えることなく、日々の仕事に着実に取り組む熱血教師的な姿勢もまた、司書教諭に求められる重要な能力である。
学校図書館における情報サービス
学校図書館のサービスは、大きく直接サービスと間接サービスに分けられる。
前者は、児童生徒や教職員にメディアや情報などを直接提供したり援助したりする諸活動のことである。
後者は、直接サービスに必要なメディアや情報を収集・整理したり、館内の環境を整備したりする諸活動のことである。
児童生徒への直接サービスには以下のものが挙げられる。
①メディア提供サービス
学校図書館が所蔵している各種のメディアを児童生徒に提供する諸活動のこと。
閲覧、貸し出し、予約・リクエストの受付などがある。
ちなみに閲覧とは、学校図書館における最も基本的な行動で、学校図書館内で読み物を読んだり、視聴覚メディアを視聴したり、インターネット接続端末を利用したりと、所蔵メディアを学校図書館内で利用すること全般を意味している。
②情報提供サービス
児童生徒が求める情報にたどりつけるように司書教諭や学校司書が援助する諸活動のことで、レファレンスサービス、レフェラルサービス、読書相談などがある。
レファレンスサービスとは、メディアの探し方がわからない、あるテーマについてどんな文献があるのか知りたいなどの情報ニーズをもつ児童生徒からのさまざまな質問や相談に対して、司書教諭や学校司書が学校図書館内の各種メディアや情報源を利用、参照して、具体的に求められた情報が記載されている箇所を提示しながら、解決できるように援助していく活動のことである。
レフェラルサービスとは、学校図書館だけでは解決が難しい質問や相談に対して、その分野の専門家や専門機関に照会して情報を入手して、あるいは専門家や専門機関を児童生徒に直接紹介して、解決できるように援助していく活動のことである。一般にレファレンスサービスの延長として行われる。
読書相談とは、児童生徒からの読書に関する質問や相談に応じるサービスのことであり、主には、読み物の選択、探索、入手の援助が中心となる。レファレンスサービスに含める考え方もある。
③図書館利用促進サービス
児童生徒に学校図書館をもっと利用してもらうように働きかける諸活動のことであり、集会(読書会、読み聞かせ会など)、行事(読書週間、読書感想文コンクールなど)、広報(図書館だより、校内放送など)、指導(利用指導、読書指導など)などがある。これらが年間を通して計画的に行われることが望ましい。
④特別な支援が必要な児童生徒に対するサービス
上述したサービスを、特別な支援が必要とする児童生徒にも等しく提供するため、独自のメディアや独自のサービスを別途用意すること。
点字図書館と連携したり、ボランティアを組織したり、館内のバリアフリー化を促進するなど。
次に、教職員へのサービスには以下のものがある。
①教育活動、授業展開に必要な資料・情報の収集と提供
授業の準備や授業展開に必要となる資料や情報を収集・提供し、教師を援助すること。
学校図書館資料の充実はもちろん、校内で分散している資料や教材の管理・把握や、優れた授業実践の記録や教材を保存し、積極的に周知、提供していくことも大切である。
また、同一地域にある他の学校図書館や公共図書館との連携や、学習支援センターの設置、さらに、教師と資料、さらには児童生徒と資料を結びつけるために、授業計画に関するアドバイスや、ティーム・ティーチングへの協力も重要な活動である。
②生活指導に必要な資料・情報の収集と提供
児童生徒の生活実態、生活の背景にあるコミュニティを理解するために役立つ資料を収集、教師に提供する。
具体的には、今日の教育問題や社会問題、地域に関する資料や情報など。
③進路指導に必要な資料・情報の収集と提供
進学・就職などに役立つ資料を収集し、提供する。
具体的には、進学先の学校の案内やシラバス、就職に関しては地域の企業、学校の特色に即した企業の要覧、説明会の資料など。
④教師の研究活動に必要な資料・情報の収集と提供
授業の教材研究や、教師個人の専門分野を伸ばすための調査や研究に必要な資料や情報を収集し、提供する。必要に応じて、大学など高等教育機関から資料を入手することもある。
⑤学校経営に必要な資料・情報の収集と提供
校務分掌や教育課程の編成、研修、教育行政などに関する資料や情報を収集し、提供する。
サービスの実施には、司書教諭だけではなく、他の教員、校長や教頭、学校事務職員と密接な連携を図る必要がある。
情報職業論覚え書き①
2018-11-01 19:43:04 (7 years ago)
-
カテゴリタグ:
- 情報
ついに来た、11月のテストラッシュ。あさっていきなり図書館司書の試験が3発来るんだけど、それより恐ろしいのは、今月中旬にある情報の試験6連発。
これは正直、持ち込み可だからなんとかなるだろと、なめていて、ほとんど準備してなかったんだけど(システム設計演習の課題を終わらせることだけに意識が向いてしまっていた)、昨夜、試験範囲が広すぎることが判明し、慌てて試験の対策にとりかかっております。
基本的に、持ち込み不可の方が試験の内容は易しいようだ。考えてみれば当然かもしれないが。
情報科教育法II(危険度☆☆)
持ち込み不可。ただし5月に受けた情報科教育法Ⅰと試験形式は似ているので、多分いける。
システム設計演習(危険度☆☆)
持ち込み不可。この前こなしたばかりだけあって、まだ記憶が残っている。多分いける。
コンピュータネットワーク(危険度☆☆☆)
持ち込み可。ブログにかなりまとめたから、まだ多少は覚えてるんだけど、内容自体はかなり専門的で警戒せねばならない。
持ち込み用ノートの作成を急ぐ。
データベースシステム(危険度☆☆☆☆)
持ち込み可。やばい。SQL文忘れた。やばい。
試験範囲がテキストの全てじゃないのが救いか。ノート作成。
情報職業論(危険度☆☆☆☆)
持ち込み可。範囲がここまで広いことを昨夜知った。メチャ準備不足。
かなりやばい。ノート作成。
ディジタル画像概論(危険度☆☆☆☆☆)
持ち込み可。レポート瞬殺科目(フォトショップを使うだけ)。
しかし、試験内容がめちゃめちゃ専門的なことを昨夜知った。メチャ準備不足。
超ヤバイ。ノート作成。
参考文献:廣石良雄著『情報と職業』
コンピュータの歴史
かつては、コンピュータに使われる論理素子の集積度によって第1世代~第4世代に分類していたが、現在では、そういったハードウェアの側面ではなく、コンピュータをどのように利用しているかという利用形態の側面で論じられることが多い。
第1世代(1940年代~):真空管
第2世代(1950年代~):トランジスタ
第3世代(1960年代~):IC(集積回路)
第3.5世代(1970年代~):LSI(大規模集積回路)
第4世代(1980年代~):VLSI、ULSI(超大規模集積回路)
黎明期(1930年代~)
コンピュータの歴史は、チューリングマシンまでさかのぼる。
これは、もともとコンピュータを開発するために作られたのではなく、ゲーデルの不完全性定理(数学の不完全性)を証明するために作られたマシンである。
チューリングは、理論上どんな計算でも解ける完璧なマシンを作り、そのマシンが解けない計算を見つければ、数学の完全性は崩れ去ると考えた。数学に何か恨みでもあったのだろうか。
このマシンを開発するに当たって、チューリングは人間が実際にどのように計算を行っているか、その手順をルールにまとめている(数字を見る→演算の記号を確認→イコールの隣に答えを書く→終了、もしくは、答えが出なかったらやり直しなど)。これこそが後のプログラムである。
①真空管コンピュータ
真空管のパルス信号で表された数値を計算するコンピュータ。
特殊な電球に過ぎない真空管には寿命があるため、やがて同様の機能があり寿命がないトランジスタにお株を奪われることになる。
ちなみにそれまでは電磁石を使っていた。
ABC(1939~42年開発)
世界最初のコンピュータといわれる。
第二次大戦中に、アイオワ州立大学のアタナソフ教授(A)とその院生ベリー(B)が開発したコンピュータ(C)。
汎用性はなく、連立一次方程式を計算するのに特化したコンピュータ。
入力はパンチカード、制御は手動で、プログラム能力はなかった。
計算の仕方は二進法。
ENIAC(1943~46年開発)
1万8000本もの真空管を用いた、幅30メートル、重さ27トンという巨大なコンピュータで、プログラムは配電盤の変更や多数のスイッチで実現したため、プログラム変更は大変だった(例えば、足し算とかけ算でケーブルの接続のパターンが違った)。
これを克服する、プログラムとデータを同じ記憶装置に格納するプログラム内蔵方式は当時すでにアイディアはあったものの、戦時中だったために完成が優先され実装されなかった。
フォン・ノイマンが開発に関わったが、出来には納得がいっていなかったらしい。
その後、ノイマンは、プログラム(演算ルール)も数値化してデータのように扱ってしまえばいいという内容のチューリングの論文を読み、大きな影響を受けた。
ちなみにENIACの計算の仕方は十進法だった。
②ノイマン型コンピュータ
チューリングの論文の影響を受けたノイマンが提唱したプログラム内蔵方式のコンピュータ。49年にはEDSACとして完成。
ノイマン型コンピュータは現在のコンピュータでも主流となっている。その特徴は、プログラムとデータを、主記憶装置に一旦格納してから実行(プログラム内蔵方式)、プログラムに書かれた命令をひとつずつ実行(逐次制御方式)、0と1の計算によって実行(二進数処理)の3つである。
メインフレーム時代(1950年代~)
メインフレームとは複数の利用者が共有する中央計算機のこと。これに他の計算器を複数接続して、その力をみんなで共用していた。
ENIAC以来、計算機は大学や研究所が中心となって開発した。IBMなど民間のメーカーも生まれたが、処理形態がバッチ処理(一括処理)であり、利用者には時間や手続きの制約が多かった。
しかし、その後TSS方式が開発されたことで、利用者の利便性は向上、商用化が活性化された。
ちなみに、当時は日本のメーカーも通産省の誘導のもとメインフレームの開発競争に明け暮れていた。富士通、東芝、三菱などが戦い、80年代には富士通が日本IBMのマーケットシェアを抜いた。
①タイムシェアリング(TSS)形式
一つの処理機構において、二つ以上の処理過程の時間を細分化して交互に配置させるようにする、データ処理システムの方法のこと。
当時は、全ての機能を中央の大型コンピュータに置き、これを多くの利用者がシェアしていた。
しかし、バッチ処理では、利用者ごとのCPUの処理時間の割り当ては、運用者が周辺装置によって割り当てていた。
その処理時間を、利用者単位に自動的に分割することで(処理時間を利用者ごとにずらす)、複数の利用者が同時にコンピュータを利用できるようになった。
アイディア自体は57年頃、アメリカの計算器科学者のボブ・バーマーやジョン・マッカーシーが思いついた。
その後、59年にイギリスのコンピュータ科学者クリストファー・ストレイチーがTSSの特許を取得。
②マシンインタフェースの飛躍
人間とマシンが接触して相互に情報を交換する仕組みが向上する。
例えば、あのマウスがダグラス・エンゲルハートによって発明される。
また、彼はハイパーテキスト(文書の任意の場所に別の文書のリンクを埋め込める仕組み)や、グラフィカルユーザインタフェース(ユーザに対する情報の表示にグラフィックを多用し、大半の操作をマウスポインタで行うことができるインタフェースのこと)なども開発、コンピュータの使いやすさは飛躍的に上がった。
③ARPANET導入
アメリカ国防総省のARPAによって開発されたパケット交換方式のコンピュータネットワーク。
分散したUNIXコンピュータ同士をTCP/IPプロトコルで相互接続したもので、後のインターネットの原型になった。
④第三の波
1980年に出版されたアドルフ・トフラーの著書。農業革命、産業革命に続く第三の技術革命として情報化革命の到来を力説した。
彼の予言はかなり当たっていて、ネットショッピング、ネットオークション、ノマドワーカー、スマートコミュニティ(先端技術を用いて社会インフラを効率化・高度化した都市や地域)などは、その後現実のものとなった。
クライアント・サーバ時代(1980年代~)
80年代に入ると、パーソナルコンピュータやミニコンピュータが登場し、非常に高価なメインフレームに対して、低価格のコンピュータを企業が独自に持てるようになった。
これらの低価格コンピュータは個人や家庭にも普及し始めたが、まだIT技術者が趣味や業務として使う程度だった。
90年頃になると、コンピュータシステムのダウンサイジング、オープン化(標準化)によって、クライアント・サーバシステムが一般化していった。
このシステムにより、クライアント側からサーバにデータを要求し、得られたデータを使ってクライアント側でも処理ができるようになった。
そのため、クライアント側で分散して行われた処理やデータをどのように集約し、管理するかという問題が発生した。
さまざまな種類のコンピュータ資源をひとつのコンピュータとして利用できないかというアイディアは、後のクラウドコンピューティングにつながる。
サーバにはUNIX系コンピュータ、クライアントPCにはウィンドウズやマッキントッシュが使用されたが、年々画面表示の機能や各種の処理機能が向上し、メインフレーム時代の処理の集中から、処理の分散へ時代は移り変わっていった。
①ビル・ゲイツの登場
ビル・ゲイツは75年4月にポール・アレンとマイクロソフト社を設立し、その後、同社を世界的企業へと成長させた。
82年からマイクロソフト社がメーカーにOEM(相手企業に自社ブランドを製造させること)提供を開始したOSがMS-DOSであり、各社の各機種のPCに移植された。
さらに、85年にはWindowsを発表した。当時は独立したOSではなくグラフィカルインタフェースを実現するアプリケーションであったが、90年代後半以降は世界中のPCの大半に搭載されるようになった。
Windowsは、その後さまざまなシリーズが発表され、GUI機能、マルチタスク機能、ネットワーク機能などを企業だけでなく個人にも浸透させた。
②Macintosh発売
アップルが開発と販売を行っているPCで、84年1月に発売が開始された。
Windows搭載のPCとともに世界中の主流となっているが、特に使い勝手を重視した設計思想を持ち、デザイン、音楽、映像などの分野や、それを利用した教育分野に多く使用されている。
Webコンピューティング時代(1990年代~)
①www概念の提案
89年イギリスのコンピュータ技術者バーナーズ・リーがグローバル・ハイパーテキスト・プロジェクトを提案し、後にwwwの概念として知られる仕組みや環境を構築した。
94年リーは、アメリカのマサチューセッツ大学のコンピュータ科学研究所に移り、wwwの各種技術の標準化を推進するために、非営利団体のW3コンソーシアムを創設、HTML、URL、HTTPなどwwwの基礎となるプロトコルを規定した。
②Java言語の開発
95年にアメリカのサン・マイクロシステムズ社がC++をもとに開発したオブジェクト指向言語がJavaである。
もともとは90年に同社の若いプログラマ(パトリック・ノートン)がJavaに発展するプログラミング言語の素案を書いた。
JavaはJava仮想マシン(Javaのバイトコードをそのプラットフォーム固有の形式に変換して実行するソフトウェア)を実装した環境であれば、異なるハードウェアや異なるOSでプログラムを稼働できるため、インターネットで動作するウェブアプリケーションの言語にはうってつけであった。
③Mosaic発表
ネットワークに接続されるPCの数は膨大になり、クライアントPCにアプリケーションやデータを配布して、サーバ側で処理を行うという方法は事実上、不可能になった。
これを解消したのが、PC標準で装備されるようになっていたWebブラウザ(Webページを閲覧するためのアプリケーションソフト)である。
Mosaicは、93年にアメリカ国立スーパーコンピュータ応用研究所からリリースされたWebブラウザで、テキストと画像を同一のウインドウ内に自動的に編集し表示することができた最初のブラウザだった。
④Netscapeブラウザ
ネスケの愛称で親しまれたブラウザ。
90年代はWebブラウザといえば、このネットスケープ・ナビゲータであったが、マイクロソフト社のInternet Explorerや、ほかのブラウザにシェアを奪われ、2008年2月にサポートは終了した。
超懐かしい。
⑤Windows95発表
Windows3.1の後継として95年に発表されたOSである。
インターネットに必要な通信プロトコルのTCP/IPを選択することができた。
Win32と呼ばれるAPI(あるソフトウェアの機能や管理するデータなどを、外部のほかのプログラムから呼び出して利用するための手順やデータ形式を定めた規約のこと)搭載のほか、消費者向けOSとして充実した機能を持っていた。
⑥ハイパーテキスト対応大規模ウェブ検索エンジン
利用者が知りたい情報をWeb上で探し出すことは、いかにコンピュータやネットワークの性能が向上したとはいえ、大変である。
このような検索を簡単に行うのが検索エンジンである。
90年代後半、ヤフーが検索エンジン界では圧倒的強さを誇っていたが、それに対抗したのが98年に創立されたグーグルであり、98年発表の『ハイパーテキスト対応大規模ウェブ検索エンジンの分析』という論文の中で、グーグルの検索エンジンに対する考え方が説明されている。
クラウドコンピューティング時代(2000年代~)
Webコンピューティングの進展により、不特定複数の企業や個人がネットワークを通じてサービスを提供するビジネスモデルが確立されてきた。
アメリカ国立標準技術研究所(NIST)は、クラウドコンピューティングを「ネットワーク、サーバ、ストレージ、アプリケーション、サービスなどの構成可能なコンピューティングリソースの共用プールに対して、便利かつオンデマンドにアクセスでき、最小の管理労力またはサービスプロバイダ間の相互動作によって迅速に提供され利用できるという、モデルの1つ」と定義している。
クラウドは、コンピュータネットワークを空に浮かぶ雲に例えた言葉である。
雲のどこかに、ユーザが利用したい時、利用したい分だけの利用料金で、サーバマシンやシステム開発環境やアプリケーションなどを提供してくれるものがある、というイメージである。
①インターネットのプラットフォーム化
クラウドはインターネットでつながれた資源を、あたかもひとまとまりのコンピュータとして扱う。
インターネットをOSのようにプラットフォーム化し、クラウド市場を進展させた技術が2005年にその言葉が使われ出したAjaxである。
AjaxはWebブラウザに実装されているJavaScriptのHTTP通信機能を使って、Webページのリロードを伴わずに、サーバとXML形式のデータのやりとりを行って処理を進めていく対話型Webアプリケーションの実装形態である。
これによって、画面遷移を伴わない動的なWebプリケーションの制作が可能になった。
②Googleクラウドを提唱
2006年、グーグル社CEOエリック・シュミットが、自社のサービス群を「クラウドコンピューティング」と表現したことが、クラウドという言葉の誕生といわれる。
③各社クラウド事業参入
先駆的な会社は、グーグル、マイクロソフト、セールスフォース・ドットコム、ヤフー、アマゾン、イーベイなどである。
④2009自治体クラウド
総務省は、平成21年度から22年度にかけて「自治体クラウド開発実証事業」を実施した。
自治体クラウドとは、自庁内にハードウェアなどを設置せず、あらかじめ事業者が所有するデータセンタに設置されたハードウェアおよびソフトウェアなどから、インターネットや専用線などのネットワークを経由してサービスを利用することで、クラウドコンピューティング技術の進展や普及をふまえた情報システムの地方導入を行うことを指している。
複数の地方公共団体が一体となって、情報システムの共有化と集約化を進めることで、運用経費の削減を図ることが目的とされた。
これは正直、持ち込み可だからなんとかなるだろと、なめていて、ほとんど準備してなかったんだけど(システム設計演習の課題を終わらせることだけに意識が向いてしまっていた)、昨夜、試験範囲が広すぎることが判明し、慌てて試験の対策にとりかかっております。
基本的に、持ち込み不可の方が試験の内容は易しいようだ。考えてみれば当然かもしれないが。
情報科教育法II(危険度☆☆)
持ち込み不可。ただし5月に受けた情報科教育法Ⅰと試験形式は似ているので、多分いける。
システム設計演習(危険度☆☆)
持ち込み不可。この前こなしたばかりだけあって、まだ記憶が残っている。多分いける。
コンピュータネットワーク(危険度☆☆☆)
持ち込み可。ブログにかなりまとめたから、まだ多少は覚えてるんだけど、内容自体はかなり専門的で警戒せねばならない。
持ち込み用ノートの作成を急ぐ。
データベースシステム(危険度☆☆☆☆)
持ち込み可。やばい。SQL文忘れた。やばい。
試験範囲がテキストの全てじゃないのが救いか。ノート作成。
情報職業論(危険度☆☆☆☆)
持ち込み可。範囲がここまで広いことを昨夜知った。メチャ準備不足。
かなりやばい。ノート作成。
ディジタル画像概論(危険度☆☆☆☆☆)
持ち込み可。レポート瞬殺科目(フォトショップを使うだけ)。
しかし、試験内容がめちゃめちゃ専門的なことを昨夜知った。メチャ準備不足。
超ヤバイ。ノート作成。
参考文献:廣石良雄著『情報と職業』
コンピュータの歴史
かつては、コンピュータに使われる論理素子の集積度によって第1世代~第4世代に分類していたが、現在では、そういったハードウェアの側面ではなく、コンピュータをどのように利用しているかという利用形態の側面で論じられることが多い。
第1世代(1940年代~):真空管
第2世代(1950年代~):トランジスタ
第3世代(1960年代~):IC(集積回路)
第3.5世代(1970年代~):LSI(大規模集積回路)
第4世代(1980年代~):VLSI、ULSI(超大規模集積回路)
黎明期(1930年代~)
コンピュータの歴史は、チューリングマシンまでさかのぼる。
これは、もともとコンピュータを開発するために作られたのではなく、ゲーデルの不完全性定理(数学の不完全性)を証明するために作られたマシンである。
チューリングは、理論上どんな計算でも解ける完璧なマシンを作り、そのマシンが解けない計算を見つければ、数学の完全性は崩れ去ると考えた。数学に何か恨みでもあったのだろうか。
このマシンを開発するに当たって、チューリングは人間が実際にどのように計算を行っているか、その手順をルールにまとめている(数字を見る→演算の記号を確認→イコールの隣に答えを書く→終了、もしくは、答えが出なかったらやり直しなど)。これこそが後のプログラムである。
①真空管コンピュータ
真空管のパルス信号で表された数値を計算するコンピュータ。
特殊な電球に過ぎない真空管には寿命があるため、やがて同様の機能があり寿命がないトランジスタにお株を奪われることになる。
ちなみにそれまでは電磁石を使っていた。
ABC(1939~42年開発)
世界最初のコンピュータといわれる。
第二次大戦中に、アイオワ州立大学のアタナソフ教授(A)とその院生ベリー(B)が開発したコンピュータ(C)。
汎用性はなく、連立一次方程式を計算するのに特化したコンピュータ。
入力はパンチカード、制御は手動で、プログラム能力はなかった。
計算の仕方は二進法。
ENIAC(1943~46年開発)
1万8000本もの真空管を用いた、幅30メートル、重さ27トンという巨大なコンピュータで、プログラムは配電盤の変更や多数のスイッチで実現したため、プログラム変更は大変だった(例えば、足し算とかけ算でケーブルの接続のパターンが違った)。
これを克服する、プログラムとデータを同じ記憶装置に格納するプログラム内蔵方式は当時すでにアイディアはあったものの、戦時中だったために完成が優先され実装されなかった。
フォン・ノイマンが開発に関わったが、出来には納得がいっていなかったらしい。
その後、ノイマンは、プログラム(演算ルール)も数値化してデータのように扱ってしまえばいいという内容のチューリングの論文を読み、大きな影響を受けた。
ちなみにENIACの計算の仕方は十進法だった。
②ノイマン型コンピュータ
チューリングの論文の影響を受けたノイマンが提唱したプログラム内蔵方式のコンピュータ。49年にはEDSACとして完成。
ノイマン型コンピュータは現在のコンピュータでも主流となっている。その特徴は、プログラムとデータを、主記憶装置に一旦格納してから実行(プログラム内蔵方式)、プログラムに書かれた命令をひとつずつ実行(逐次制御方式)、0と1の計算によって実行(二進数処理)の3つである。
メインフレーム時代(1950年代~)
メインフレームとは複数の利用者が共有する中央計算機のこと。これに他の計算器を複数接続して、その力をみんなで共用していた。
ENIAC以来、計算機は大学や研究所が中心となって開発した。IBMなど民間のメーカーも生まれたが、処理形態がバッチ処理(一括処理)であり、利用者には時間や手続きの制約が多かった。
しかし、その後TSS方式が開発されたことで、利用者の利便性は向上、商用化が活性化された。
ちなみに、当時は日本のメーカーも通産省の誘導のもとメインフレームの開発競争に明け暮れていた。富士通、東芝、三菱などが戦い、80年代には富士通が日本IBMのマーケットシェアを抜いた。
①タイムシェアリング(TSS)形式
一つの処理機構において、二つ以上の処理過程の時間を細分化して交互に配置させるようにする、データ処理システムの方法のこと。
当時は、全ての機能を中央の大型コンピュータに置き、これを多くの利用者がシェアしていた。
しかし、バッチ処理では、利用者ごとのCPUの処理時間の割り当ては、運用者が周辺装置によって割り当てていた。
その処理時間を、利用者単位に自動的に分割することで(処理時間を利用者ごとにずらす)、複数の利用者が同時にコンピュータを利用できるようになった。
アイディア自体は57年頃、アメリカの計算器科学者のボブ・バーマーやジョン・マッカーシーが思いついた。
その後、59年にイギリスのコンピュータ科学者クリストファー・ストレイチーがTSSの特許を取得。
②マシンインタフェースの飛躍
人間とマシンが接触して相互に情報を交換する仕組みが向上する。
例えば、あのマウスがダグラス・エンゲルハートによって発明される。
また、彼はハイパーテキスト(文書の任意の場所に別の文書のリンクを埋め込める仕組み)や、グラフィカルユーザインタフェース(ユーザに対する情報の表示にグラフィックを多用し、大半の操作をマウスポインタで行うことができるインタフェースのこと)なども開発、コンピュータの使いやすさは飛躍的に上がった。
③ARPANET導入
アメリカ国防総省のARPAによって開発されたパケット交換方式のコンピュータネットワーク。
分散したUNIXコンピュータ同士をTCP/IPプロトコルで相互接続したもので、後のインターネットの原型になった。
④第三の波
1980年に出版されたアドルフ・トフラーの著書。農業革命、産業革命に続く第三の技術革命として情報化革命の到来を力説した。
彼の予言はかなり当たっていて、ネットショッピング、ネットオークション、ノマドワーカー、スマートコミュニティ(先端技術を用いて社会インフラを効率化・高度化した都市や地域)などは、その後現実のものとなった。
クライアント・サーバ時代(1980年代~)
80年代に入ると、パーソナルコンピュータやミニコンピュータが登場し、非常に高価なメインフレームに対して、低価格のコンピュータを企業が独自に持てるようになった。
これらの低価格コンピュータは個人や家庭にも普及し始めたが、まだIT技術者が趣味や業務として使う程度だった。
90年頃になると、コンピュータシステムのダウンサイジング、オープン化(標準化)によって、クライアント・サーバシステムが一般化していった。
このシステムにより、クライアント側からサーバにデータを要求し、得られたデータを使ってクライアント側でも処理ができるようになった。
そのため、クライアント側で分散して行われた処理やデータをどのように集約し、管理するかという問題が発生した。
さまざまな種類のコンピュータ資源をひとつのコンピュータとして利用できないかというアイディアは、後のクラウドコンピューティングにつながる。
サーバにはUNIX系コンピュータ、クライアントPCにはウィンドウズやマッキントッシュが使用されたが、年々画面表示の機能や各種の処理機能が向上し、メインフレーム時代の処理の集中から、処理の分散へ時代は移り変わっていった。
①ビル・ゲイツの登場
ビル・ゲイツは75年4月にポール・アレンとマイクロソフト社を設立し、その後、同社を世界的企業へと成長させた。
82年からマイクロソフト社がメーカーにOEM(相手企業に自社ブランドを製造させること)提供を開始したOSがMS-DOSであり、各社の各機種のPCに移植された。
さらに、85年にはWindowsを発表した。当時は独立したOSではなくグラフィカルインタフェースを実現するアプリケーションであったが、90年代後半以降は世界中のPCの大半に搭載されるようになった。
Windowsは、その後さまざまなシリーズが発表され、GUI機能、マルチタスク機能、ネットワーク機能などを企業だけでなく個人にも浸透させた。
②Macintosh発売
アップルが開発と販売を行っているPCで、84年1月に発売が開始された。
Windows搭載のPCとともに世界中の主流となっているが、特に使い勝手を重視した設計思想を持ち、デザイン、音楽、映像などの分野や、それを利用した教育分野に多く使用されている。
Webコンピューティング時代(1990年代~)
①www概念の提案
89年イギリスのコンピュータ技術者バーナーズ・リーがグローバル・ハイパーテキスト・プロジェクトを提案し、後にwwwの概念として知られる仕組みや環境を構築した。
94年リーは、アメリカのマサチューセッツ大学のコンピュータ科学研究所に移り、wwwの各種技術の標準化を推進するために、非営利団体のW3コンソーシアムを創設、HTML、URL、HTTPなどwwwの基礎となるプロトコルを規定した。
②Java言語の開発
95年にアメリカのサン・マイクロシステムズ社がC++をもとに開発したオブジェクト指向言語がJavaである。
もともとは90年に同社の若いプログラマ(パトリック・ノートン)がJavaに発展するプログラミング言語の素案を書いた。
JavaはJava仮想マシン(Javaのバイトコードをそのプラットフォーム固有の形式に変換して実行するソフトウェア)を実装した環境であれば、異なるハードウェアや異なるOSでプログラムを稼働できるため、インターネットで動作するウェブアプリケーションの言語にはうってつけであった。
③Mosaic発表
ネットワークに接続されるPCの数は膨大になり、クライアントPCにアプリケーションやデータを配布して、サーバ側で処理を行うという方法は事実上、不可能になった。
これを解消したのが、PC標準で装備されるようになっていたWebブラウザ(Webページを閲覧するためのアプリケーションソフト)である。
Mosaicは、93年にアメリカ国立スーパーコンピュータ応用研究所からリリースされたWebブラウザで、テキストと画像を同一のウインドウ内に自動的に編集し表示することができた最初のブラウザだった。
④Netscapeブラウザ
ネスケの愛称で親しまれたブラウザ。
90年代はWebブラウザといえば、このネットスケープ・ナビゲータであったが、マイクロソフト社のInternet Explorerや、ほかのブラウザにシェアを奪われ、2008年2月にサポートは終了した。
超懐かしい。
⑤Windows95発表
Windows3.1の後継として95年に発表されたOSである。
インターネットに必要な通信プロトコルのTCP/IPを選択することができた。
Win32と呼ばれるAPI(あるソフトウェアの機能や管理するデータなどを、外部のほかのプログラムから呼び出して利用するための手順やデータ形式を定めた規約のこと)搭載のほか、消費者向けOSとして充実した機能を持っていた。
⑥ハイパーテキスト対応大規模ウェブ検索エンジン
利用者が知りたい情報をWeb上で探し出すことは、いかにコンピュータやネットワークの性能が向上したとはいえ、大変である。
このような検索を簡単に行うのが検索エンジンである。
90年代後半、ヤフーが検索エンジン界では圧倒的強さを誇っていたが、それに対抗したのが98年に創立されたグーグルであり、98年発表の『ハイパーテキスト対応大規模ウェブ検索エンジンの分析』という論文の中で、グーグルの検索エンジンに対する考え方が説明されている。
クラウドコンピューティング時代(2000年代~)
Webコンピューティングの進展により、不特定複数の企業や個人がネットワークを通じてサービスを提供するビジネスモデルが確立されてきた。
アメリカ国立標準技術研究所(NIST)は、クラウドコンピューティングを「ネットワーク、サーバ、ストレージ、アプリケーション、サービスなどの構成可能なコンピューティングリソースの共用プールに対して、便利かつオンデマンドにアクセスでき、最小の管理労力またはサービスプロバイダ間の相互動作によって迅速に提供され利用できるという、モデルの1つ」と定義している。
クラウドは、コンピュータネットワークを空に浮かぶ雲に例えた言葉である。
雲のどこかに、ユーザが利用したい時、利用したい分だけの利用料金で、サーバマシンやシステム開発環境やアプリケーションなどを提供してくれるものがある、というイメージである。
①インターネットのプラットフォーム化
クラウドはインターネットでつながれた資源を、あたかもひとまとまりのコンピュータとして扱う。
インターネットをOSのようにプラットフォーム化し、クラウド市場を進展させた技術が2005年にその言葉が使われ出したAjaxである。
AjaxはWebブラウザに実装されているJavaScriptのHTTP通信機能を使って、Webページのリロードを伴わずに、サーバとXML形式のデータのやりとりを行って処理を進めていく対話型Webアプリケーションの実装形態である。
これによって、画面遷移を伴わない動的なWebプリケーションの制作が可能になった。
②Googleクラウドを提唱
2006年、グーグル社CEOエリック・シュミットが、自社のサービス群を「クラウドコンピューティング」と表現したことが、クラウドという言葉の誕生といわれる。
③各社クラウド事業参入
先駆的な会社は、グーグル、マイクロソフト、セールスフォース・ドットコム、ヤフー、アマゾン、イーベイなどである。
④2009自治体クラウド
総務省は、平成21年度から22年度にかけて「自治体クラウド開発実証事業」を実施した。
自治体クラウドとは、自庁内にハードウェアなどを設置せず、あらかじめ事業者が所有するデータセンタに設置されたハードウェアおよびソフトウェアなどから、インターネットや専用線などのネットワークを経由してサービスを利用することで、クラウドコンピューティング技術の進展や普及をふまえた情報システムの地方導入を行うことを指している。
複数の地方公共団体が一体となって、情報システムの共有化と集約化を進めることで、運用経費の削減を図ることが目的とされた。
システム設計演習覚え書き④
2018-10-28 18:13:32 (7 years ago)
-
カテゴリタグ:
- 情報
とりあえず必修課題は全て終わりました・・・!\(^o^)/
とはいえ、試験の加点対象になるオマケの課題がまだ9個あって、そのうち3個はできたんだけど、残り6個は仮想マシンで動かさなきゃいけないやつで、この仮想マシンが私の家のネット環境だとオーバーテクノロジーで、まあ、止まる止まる。ぷーあらあら(どせいさん)。みたいな。
で、調べてみたら、オマケを3問やってたった1点の加点ということで、まあ、諦めて(え)、今日の午後は、来月中旬のテスト勉強をしてました。
でも、まあ、残りの6問も気持ちが悪いから、今度気が向いたらネットカフェとかに行ってやってみるかもしれない。
それでは、今までのシステム設計の一ヶ月ちょいの軌跡を振り返ってみましょう。
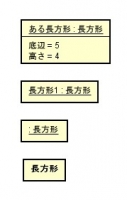
クラスとインスタンス
クラス図とインスタンス図はデザインがそっくりなので、インスタンスの名前の部分には必ず下線をつけて区別する!
継承
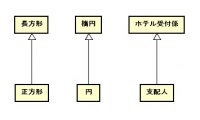
どちらが一般的で、どちらが特殊かを考える。
例えば、正方形は特殊な長方形なので、包含記号を使うと「長方形⊃正方形」となる。論理記号の矢印のデザインは⇒で、クラス図の矢印はチビ太のおでんのようなデザインなのに注意。
ポリモーフィズム
同じ呼び方(メッセージ)の操作で異なる動作をさせること。
例えば、一から作るのではなく、既存のシステムの操作をすこし修正=上書き(オーバーライド)すれば事足りそうな場合など。
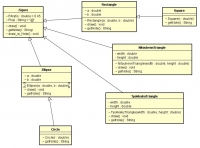
抽象クラス
抽象クラスには実態がないため、例えば「図形」という抽象クラスがあった場合、その具体例であるインスタンスは作れない。
これが、「長方形」や「楕円」などの具体的な図形のクラスではいろいろなインスタンス(いろいろな形の長方形や楕円)が作れる。
関連
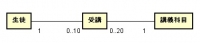
多重度が重要。アスタリスクのマークは任意の数。
頻出する関連パターンは「モノ」-「コト」ー「コト」で、多重度は「1対*」「*対1」が多い。
特にこの問題が危険。
生徒にとっては、受講できる科目は最大10科目なので、0..10となる。
講義科目にとっては、受講する生徒の数は最大20人なので0..20となる。
依存
依存を示す矢印は点線で、さきっちょは^で、黒い三角形▲ではないのに注意。
依存するクラスは変更できるが、依存される側を変えると、そいつに依存している奴にも影響が及ぶ。
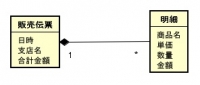
コンポジション関連
販売伝票の情報から、明細というクラスを作りデータを分ける。
販売伝票に共通するデータは「日時」「支店名」「合計金額」なので、これらは販売伝票のクラスに残す。
それ以外の何を何個買ったかのデータ「商品名」「単価」「数量」「金額」は、明細のクラスに送る。
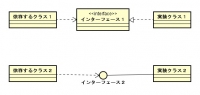
実装
依存はさきっちょが^の点線の矢印だったが、実装はさきっちょが△の点線の矢印。
そういや、実習課題で実装の矢印ってあんまり使わなかった気がする。
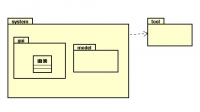
パッケージ図
関連性の高いデータや操作は一つのパッケージに入れてしまう。
例えば、「マグロ」「カンパチ」「ヒラメ」などのデータは「寿司ネタ」というパッケージに入れるとわかりやすい。
また、パッケージ内のデータは可視性の設定によって、表示・非表示が可能。非表示設定にすると、そのデータは他のパッケージから見えなくなる。
表示は+のマーク、非表示は~なので注意。
シーケンス図
課題を進めるにつれ最終的にすごい複雑になった奴。
例えばこれ。
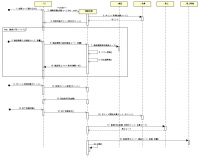
ちなみに、シーケンス図の作成には、まずクラス図(設計図)を作成しなければならない。
また、あるクラスの処理は、そのクラスを指すメッセージの矢印によって行われるのに注意(逆に言うとメッセージの矢印に書かれている操作内容は、矢印が刺さっているクラスが持っている!)。
さらに、同期メッセージの矢印の先っちょは▲、非同期メッセージの矢印の先っちょは^なのも注意する(これを混同すると実行仕様=活性区間を示す縦長の四角形が連動して勝手に大きくなっちゃう)。
要件定義
要件定義は、顧客と開発者の共同作業で考える。
まず現状を分析し、顧客からシステム要求を聞き、それを元に開発者が分析結果(要件定義書)を提示して、共通理解を図る。
顧客は、依頼者やエンドユーザのことで、これがステークホルダーになると、もう少し広く、開発側も含まれる。
要件定義のうち、必ず搭載すべき機能は機能要件と呼ばれるが、反応速度といったユーザビリティや、故障しにくいといった信頼性、セキュリティなど、顧客の要件にはない機能(性能)である非機能要件が昨今取りざたされている。これは要件定義書に明記されてはいないため、限られた時間と資金の中、顧客の気持ちをどれだけ忖度できるかが、顧客の満足度を高めるという。
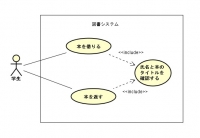
ユースケース図
ユーザの要求に、どのようにシステムが対応するかを示す図のこと。
従って、まずアクターを抽出しなければならない。
例えば、コンビニのレジシステムの場合、それを扱うアクターはレジ係と店長(店長もレジは使えるから)であり、お客さんではない。
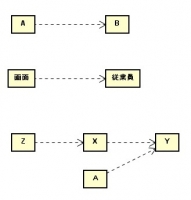
以下は、学生が図書館で本を借りる際のユースケース図。
なお、「氏名と本のタイトルを確認する」の手順のように、「本を借りる」ときにも「本を返す」ときにも行われるようなものは、〈〈include〉〉の矢印で指し示す。
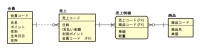
ER図
マイクル・クライトン先生の緊急救命室ではない。
エンティティ・リレーションシップ・ダイアグラムの略。
エンティティとは実体とか概念のことで、複数の対象物を共通のカテゴリーでまとめた四角形と考えて良い。
これはUMLでいうクラスに相当するため、クラス図をER図に変換することができる。
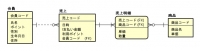
クラス図との違いは、クラス名(エンティティ名)が四角形の外に追いやられ、1段目のマスにはRDBSのように主キーが入ること。
さらに、「学生」や「本」のように一意(ユニーク)に求められるものは親エンティティ、「貸出」のように様々なパターンがあるものは子エンティティと呼ばれる。
これら親子をつなぐ多重度のマークも覚えなければならない。
鳥の足(クロウズ・フット)のマークは複数という意味。
|は1つ、○は0つ、エンティティにつながっているという意味。
ちなみに|と○を合体させると0か1という意味。
また、子エンティティが親エンティティに依存している場合、子エンティティの四角形の角は丸くなる。
とはいえ、試験の加点対象になるオマケの課題がまだ9個あって、そのうち3個はできたんだけど、残り6個は仮想マシンで動かさなきゃいけないやつで、この仮想マシンが私の家のネット環境だとオーバーテクノロジーで、まあ、止まる止まる。ぷーあらあら(どせいさん)。みたいな。
で、調べてみたら、オマケを3問やってたった1点の加点ということで、まあ、諦めて(え)、今日の午後は、来月中旬のテスト勉強をしてました。
でも、まあ、残りの6問も気持ちが悪いから、今度気が向いたらネットカフェとかに行ってやってみるかもしれない。
それでは、今までのシステム設計の一ヶ月ちょいの軌跡を振り返ってみましょう。
クラスとインスタンス
クラス図とインスタンス図はデザインがそっくりなので、インスタンスの名前の部分には必ず下線をつけて区別する!

継承
どちらが一般的で、どちらが特殊かを考える。
例えば、正方形は特殊な長方形なので、包含記号を使うと「長方形⊃正方形」となる。論理記号の矢印のデザインは⇒で、クラス図の矢印はチビ太のおでんのようなデザインなのに注意。

ポリモーフィズム
同じ呼び方(メッセージ)の操作で異なる動作をさせること。
例えば、一から作るのではなく、既存のシステムの操作をすこし修正=上書き(オーバーライド)すれば事足りそうな場合など。
抽象クラス
抽象クラスには実態がないため、例えば「図形」という抽象クラスがあった場合、その具体例であるインスタンスは作れない。
これが、「長方形」や「楕円」などの具体的な図形のクラスではいろいろなインスタンス(いろいろな形の長方形や楕円)が作れる。

関連
多重度が重要。アスタリスクのマークは任意の数。
頻出する関連パターンは「モノ」-「コト」ー「コト」で、多重度は「1対*」「*対1」が多い。
特にこの問題が危険。
生徒にとっては、受講できる科目は最大10科目なので、0..10となる。
講義科目にとっては、受講する生徒の数は最大20人なので0..20となる。
依存
依存を示す矢印は点線で、さきっちょは^で、黒い三角形▲ではないのに注意。
依存するクラスは変更できるが、依存される側を変えると、そいつに依存している奴にも影響が及ぶ。

コンポジション関連
販売伝票の情報から、明細というクラスを作りデータを分ける。
販売伝票に共通するデータは「日時」「支店名」「合計金額」なので、これらは販売伝票のクラスに残す。
それ以外の何を何個買ったかのデータ「商品名」「単価」「数量」「金額」は、明細のクラスに送る。

実装
依存はさきっちょが^の点線の矢印だったが、実装はさきっちょが△の点線の矢印。
そういや、実習課題で実装の矢印ってあんまり使わなかった気がする。

パッケージ図
関連性の高いデータや操作は一つのパッケージに入れてしまう。
例えば、「マグロ」「カンパチ」「ヒラメ」などのデータは「寿司ネタ」というパッケージに入れるとわかりやすい。
また、パッケージ内のデータは可視性の設定によって、表示・非表示が可能。非表示設定にすると、そのデータは他のパッケージから見えなくなる。
表示は+のマーク、非表示は~なので注意。

シーケンス図
課題を進めるにつれ最終的にすごい複雑になった奴。
例えばこれ。

ちなみに、シーケンス図の作成には、まずクラス図(設計図)を作成しなければならない。
また、あるクラスの処理は、そのクラスを指すメッセージの矢印によって行われるのに注意(逆に言うとメッセージの矢印に書かれている操作内容は、矢印が刺さっているクラスが持っている!)。
さらに、同期メッセージの矢印の先っちょは▲、非同期メッセージの矢印の先っちょは^なのも注意する(これを混同すると実行仕様=活性区間を示す縦長の四角形が連動して勝手に大きくなっちゃう)。
要件定義
要件定義は、顧客と開発者の共同作業で考える。
まず現状を分析し、顧客からシステム要求を聞き、それを元に開発者が分析結果(要件定義書)を提示して、共通理解を図る。
顧客は、依頼者やエンドユーザのことで、これがステークホルダーになると、もう少し広く、開発側も含まれる。
要件定義のうち、必ず搭載すべき機能は機能要件と呼ばれるが、反応速度といったユーザビリティや、故障しにくいといった信頼性、セキュリティなど、顧客の要件にはない機能(性能)である非機能要件が昨今取りざたされている。これは要件定義書に明記されてはいないため、限られた時間と資金の中、顧客の気持ちをどれだけ忖度できるかが、顧客の満足度を高めるという。
ユースケース図
ユーザの要求に、どのようにシステムが対応するかを示す図のこと。
従って、まずアクターを抽出しなければならない。
例えば、コンビニのレジシステムの場合、それを扱うアクターはレジ係と店長(店長もレジは使えるから)であり、お客さんではない。
以下は、学生が図書館で本を借りる際のユースケース図。
なお、「氏名と本のタイトルを確認する」の手順のように、「本を借りる」ときにも「本を返す」ときにも行われるようなものは、〈〈include〉〉の矢印で指し示す。

ER図
マイクル・クライトン先生の緊急救命室ではない。
エンティティ・リレーションシップ・ダイアグラムの略。
エンティティとは実体とか概念のことで、複数の対象物を共通のカテゴリーでまとめた四角形と考えて良い。
これはUMLでいうクラスに相当するため、クラス図をER図に変換することができる。

クラス図との違いは、クラス名(エンティティ名)が四角形の外に追いやられ、1段目のマスにはRDBSのように主キーが入ること。
さらに、「学生」や「本」のように一意(ユニーク)に求められるものは親エンティティ、「貸出」のように様々なパターンがあるものは子エンティティと呼ばれる。
これら親子をつなぐ多重度のマークも覚えなければならない。
鳥の足(クロウズ・フット)のマークは複数という意味。
|は1つ、○は0つ、エンティティにつながっているという意味。
ちなみに|と○を合体させると0か1という意味。
また、子エンティティが親エンティティに依存している場合、子エンティティの四角形の角は丸くなる。

システム設計演習覚え書き③
2018-10-24 18:40:11 (7 years ago)
-
カテゴリタグ:
- 情報
最近気が向いて順調に攻略中のシステム設計。残る必修課題は12個。なんとか今月中にいけそうだ!やれば出来る子!!
参考文献:内山俊郎著『わかりやすい情報システムの設計――UML/Javaを用いた演習』
開発プロセス
情報システムの開発プロセスには、大きく二つの方法がある。
順番に手順を完了させるウォーターフォール型と、部分的なリリースを繰り返して完成度を上げていく反復型である。
この二大派閥は、どちらが優れていて、どちらが劣っていると、決めつけることはできず、また、仮に反復型が優れていたとしても、明日から反復型にします!と簡単に切り替えられない現実的な問題もある。
ウォーターフォール型
要件定義→設計→実装と、滝が流れるように順次処理をする。
滝の水が逆流しないように、プロセスは後戻りしない。
そのため、事前に綿密な計画(いつまでに何を作るか、コストの見積はいくらか)を立てる。基本的に手順のルールがしっかりと決まっている。
開発期間は数ヶ月~数年で、もちろん最終目標(スコープ=何を作るか)は変わらない。
メリット
生産性が高い。要件定義を終えれば設計を一気に進められる(中断が少ない)。
全体的な予算見積もりが早期に出る。
デメリット
対応力が低い。プロセスの初期で要件定義を終えているので、その後変更が必要になっても路線変更が難しい。実際は手順を戻ることになるが、それもできずに手遅れになることもある。
工程によってメンバーが替わるため(バトンタッチする)、引き継ぎ業務(ドキュメント作成など)が必要。
反復(イテレーション)型
非ウォーターフォール型とも呼ばれる。
システムを機能面などで小分けにし、それぞれに開発期間(1~4週間ほどの短いもの)を設ける。つまり、各開発期間で分割されたシステムの開発(全アクティビティの実行)を行う。
全体の計画は概略的。開発規模の見積もりが固まり出すのは、プロジェクト期間の10~20%が終わるくらい。つまり、定額契約が難しい。
ルールよりもエンジニアの経験がものをいうため、開発の進め方は彼らの経験とともに変わり、常に向上していく。
2000年頃普及しだしたイメージがあるが、古くには、50年代のX15極超音速ジェット機の開発、60年代のNASAにおけるマーキュリー計画、72年のトライデント潜水艦命令制御システムの開発、77~80年のスペースシャトルの第1航空電子ソフトウェアシステムの開発などの例がある。
その後、アメリカ国防省はウォーターフォール型の開発を推奨したが、失敗事例(先端技術開発では開発要求がリアルタイムで進化していってしまうため)を見て、87年の勧告では早くも反復型の推奨に戻している。
メリット
対応力が高い。いつでも軌道修正が可能。
例えば、ある機能をせっかく開発したのに結局使わなかったというような開発の無駄をなくせる。
システムを小単位ごとに分割するため開発期間が短縮できる。
工程が変わってもメンバーが替わらないため引き継ぎが不要で、また前行程での経験がチームのノウハウとして蓄積していく。
デメリット
生産性が低い(作業を途中で中断することが容易なため)。
全体的な予算の見積もりが不明確な状態でスタートするため、請負型契約(完成した仕事に報酬を支払う契約)が困難。同様に、企業の規模が大きいと予算管理部門が反復開発を採用しない。
アジャイル開発
アジャイルとは俊敏という意味(・・・もしかしてアジャコングって俊敏なゴリラっていう意味!?)。
アジャイルソフトウェア開発宣言(01年にユタ州に集まった17人のプログラマーやエンジニアが行なった宣言)と、全12項目のアジャイル原則を指針とする、反復型開発プロセスである。
アジャイル宣言
プロセスやツールよりも・・・個人と相互作用
包括的なドキュメントよりも・・・動くソフトウェア
契約交渉よりも・・・顧客との協調
計画に従うよりも・・・変化に対応すること
これは、左側の言い分にも価値はあるが、それよりも右側を重視するということである。
「個人と相互作用」からは、まず開発者が満足することが持続可能な開発において必要であることが、「顧客との協調」「変化に対応すること」からは、顧客やエンドユーザからのフィードバックを受け入れることや、コミュニケーションを重視している(スクラム開発)ことがわかる。
また、アジャイル開発には上手くいく方法の中で最もシンプルなものを選べという考え方も盛り込まれている。
スクラム(Scrum)
人命に関わるシステムの設計にも用いられているアジャイル開発の中で最も有名な手法。
ラグビーのスクラムのように、開発チームのメンバー(なぜかブタと呼ばれる)同士がコミュニケーションをよく取り合い、足並みをそろえて開発を行なう。
例えば、毎朝立ちながら20分程度のミーティング(スクラムミーティング)をするなど、反復ごとに自分たちで立案した計画を自分たちで精査する。
そのため、チームの人数は3~10人くらいに抑える(人数が多いとコミュニケーションが難しくなり、チームとしての一体感も希薄化するため)。
ちなみに、反復の途中ではメンバー以外の利害関係者が作業を追加してはならない。つまり、部外者(なぜかニワトリと呼ばれる)は口をはさまない。チームの自律性を重んじるのである。
スクラムミーティングの内容としては以下のものがある。
①前回のスクラム以降何を行ったか?
②今から次のスクラムまでに何を行うか?
③反復の目的を達成する上での障害は何か?
④スプリントバックログ(チームが当たるタスクの待ち行列のこと)に追加するタスクはあるか?
⑤チームメンバーから刺激を得て、何か新しく学んだことはあったか?
エクストリーム・プログラミング(XP)
小規模プロジェクトを素早く成功させることに特化した方法(反復期間は1~2週間)。
開発途中の仕様変更や設定変更にも勇気をもって柔軟に対応する。
プログラマー中心主義と言ってもよく、バディムービーのようにタッグを組んでプログラミングをするペアプログラミングなど面白い考え方がある。
XPが独特な点は、プログラムコードとテスト以外には成果物を要求しない点である。
他のアジャイル開発では、目前の反復の計画くらいは立てるが、XPではドキュメント作成を極力減らすため、そういったものすら作らない(ただし、ホワイトボードにタスクリストくらいは書く)。
参考文献:内山俊郎著『わかりやすい情報システムの設計――UML/Javaを用いた演習』
開発プロセス
情報システムの開発プロセスには、大きく二つの方法がある。
順番に手順を完了させるウォーターフォール型と、部分的なリリースを繰り返して完成度を上げていく反復型である。
この二大派閥は、どちらが優れていて、どちらが劣っていると、決めつけることはできず、また、仮に反復型が優れていたとしても、明日から反復型にします!と簡単に切り替えられない現実的な問題もある。
ウォーターフォール型
要件定義→設計→実装と、滝が流れるように順次処理をする。
滝の水が逆流しないように、プロセスは後戻りしない。
そのため、事前に綿密な計画(いつまでに何を作るか、コストの見積はいくらか)を立てる。基本的に手順のルールがしっかりと決まっている。
開発期間は数ヶ月~数年で、もちろん最終目標(スコープ=何を作るか)は変わらない。
メリット
生産性が高い。要件定義を終えれば設計を一気に進められる(中断が少ない)。
全体的な予算見積もりが早期に出る。
デメリット
対応力が低い。プロセスの初期で要件定義を終えているので、その後変更が必要になっても路線変更が難しい。実際は手順を戻ることになるが、それもできずに手遅れになることもある。
工程によってメンバーが替わるため(バトンタッチする)、引き継ぎ業務(ドキュメント作成など)が必要。
反復(イテレーション)型
非ウォーターフォール型とも呼ばれる。
システムを機能面などで小分けにし、それぞれに開発期間(1~4週間ほどの短いもの)を設ける。つまり、各開発期間で分割されたシステムの開発(全アクティビティの実行)を行う。
全体の計画は概略的。開発規模の見積もりが固まり出すのは、プロジェクト期間の10~20%が終わるくらい。つまり、定額契約が難しい。
ルールよりもエンジニアの経験がものをいうため、開発の進め方は彼らの経験とともに変わり、常に向上していく。
2000年頃普及しだしたイメージがあるが、古くには、50年代のX15極超音速ジェット機の開発、60年代のNASAにおけるマーキュリー計画、72年のトライデント潜水艦命令制御システムの開発、77~80年のスペースシャトルの第1航空電子ソフトウェアシステムの開発などの例がある。
その後、アメリカ国防省はウォーターフォール型の開発を推奨したが、失敗事例(先端技術開発では開発要求がリアルタイムで進化していってしまうため)を見て、87年の勧告では早くも反復型の推奨に戻している。
メリット
対応力が高い。いつでも軌道修正が可能。
例えば、ある機能をせっかく開発したのに結局使わなかったというような開発の無駄をなくせる。
システムを小単位ごとに分割するため開発期間が短縮できる。
工程が変わってもメンバーが替わらないため引き継ぎが不要で、また前行程での経験がチームのノウハウとして蓄積していく。
デメリット
生産性が低い(作業を途中で中断することが容易なため)。
全体的な予算の見積もりが不明確な状態でスタートするため、請負型契約(完成した仕事に報酬を支払う契約)が困難。同様に、企業の規模が大きいと予算管理部門が反復開発を採用しない。
アジャイル開発
アジャイルとは俊敏という意味(・・・もしかしてアジャコングって俊敏なゴリラっていう意味!?)。
アジャイルソフトウェア開発宣言(01年にユタ州に集まった17人のプログラマーやエンジニアが行なった宣言)と、全12項目のアジャイル原則を指針とする、反復型開発プロセスである。
アジャイル宣言
プロセスやツールよりも・・・個人と相互作用
包括的なドキュメントよりも・・・動くソフトウェア
契約交渉よりも・・・顧客との協調
計画に従うよりも・・・変化に対応すること
これは、左側の言い分にも価値はあるが、それよりも右側を重視するということである。
「個人と相互作用」からは、まず開発者が満足することが持続可能な開発において必要であることが、「顧客との協調」「変化に対応すること」からは、顧客やエンドユーザからのフィードバックを受け入れることや、コミュニケーションを重視している(スクラム開発)ことがわかる。
また、アジャイル開発には上手くいく方法の中で最もシンプルなものを選べという考え方も盛り込まれている。
スクラム(Scrum)
人命に関わるシステムの設計にも用いられているアジャイル開発の中で最も有名な手法。
ラグビーのスクラムのように、開発チームのメンバー(なぜかブタと呼ばれる)同士がコミュニケーションをよく取り合い、足並みをそろえて開発を行なう。
例えば、毎朝立ちながら20分程度のミーティング(スクラムミーティング)をするなど、反復ごとに自分たちで立案した計画を自分たちで精査する。
そのため、チームの人数は3~10人くらいに抑える(人数が多いとコミュニケーションが難しくなり、チームとしての一体感も希薄化するため)。
ちなみに、反復の途中ではメンバー以外の利害関係者が作業を追加してはならない。つまり、部外者(なぜかニワトリと呼ばれる)は口をはさまない。チームの自律性を重んじるのである。
スクラムミーティングの内容としては以下のものがある。
①前回のスクラム以降何を行ったか?
②今から次のスクラムまでに何を行うか?
③反復の目的を達成する上での障害は何か?
④スプリントバックログ(チームが当たるタスクの待ち行列のこと)に追加するタスクはあるか?
⑤チームメンバーから刺激を得て、何か新しく学んだことはあったか?
エクストリーム・プログラミング(XP)
小規模プロジェクトを素早く成功させることに特化した方法(反復期間は1~2週間)。
開発途中の仕様変更や設定変更にも勇気をもって柔軟に対応する。
プログラマー中心主義と言ってもよく、バディムービーのようにタッグを組んでプログラミングをするペアプログラミングなど面白い考え方がある。
XPが独特な点は、プログラムコードとテスト以外には成果物を要求しない点である。
他のアジャイル開発では、目前の反復の計画くらいは立てるが、XPではドキュメント作成を極力減らすため、そういったものすら作らない(ただし、ホワイトボードにタスクリストくらいは書く)。
- Calendar
<< January 2026 >> Sun Mon Tue Wed Thu Fri Sat 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
- search this site.
- tags
-
- 漫画 (387)
- 脚本 (243)
- 映画 (235)
- 雑記 (163)
- ゲーム (156)
- 本 (116)
- 教育 (107)
- 生物学 (105)
- 科学 (93)
- 社会学 (81)
- 歴史 (72)
- テレビ (71)
- 芸術 (61)
- 政治 (50)
- 数学 (40)
- 進化論 (40)
- 資格試験 (38)
- 情報 (38)
- サイト・ブログ (37)
- 語学 (37)
- 映画論 (36)
- 物理学 (33)
- 哲学 (32)
- 恐竜 (29)
- 育児 (28)
- 文学 (26)
- 化学 (25)
- 論文 (22)
- PIXAR (22)
- 心理学 (18)
- 地学 (16)
- 気象学 (15)
- 地理学 (15)
- 技術 (13)
- 経済学 (12)
- 医学 (11)
- 玩具 (9)
- 司書 (8)
- 法律学 (7)
- 対談 (5)
- スポーツ (4)
- 映画の評価について (1)
- プロフィール (1)
- archives
-
- 202601 (2)
- 202512 (4)
- 202511 (15)
- 202510 (8)
- 202509 (5)
- 202508 (3)
- 202507 (3)
- 202506 (3)
- 202505 (1)
- 202504 (2)
- 202503 (2)
- 202502 (2)
- 202501 (1)
- 202412 (2)
- 202411 (6)
- 202410 (2)
- 202409 (4)
- 202408 (4)
- 202407 (7)
- 202406 (27)
- 202405 (11)
- 202404 (4)
- 202403 (23)
- 202402 (22)
- 202401 (15)
- 202312 (4)
- 202311 (7)
- 202310 (2)
- 202309 (8)
- 202308 (9)
- 202307 (8)
- 202306 (5)
- 202305 (15)
- 202304 (4)
- 202303 (4)
- 202302 (2)
- 202301 (4)
- 202212 (15)
- 202211 (7)
- 202210 (5)
- 202209 (4)
- 202208 (4)
- 202207 (7)
- 202206 (2)
- 202205 (5)
- 202204 (3)
- 202203 (2)
- 202202 (5)
- 202201 (6)
- 202112 (6)
- 202111 (4)
- 202110 (6)
- 202109 (7)
- 202108 (5)
- 202107 (8)
- 202106 (4)
- 202105 (8)
- 202104 (4)
- 202103 (6)
- 202102 (10)
- 202101 (3)
- 202012 (12)
- 202011 (3)
- 202010 (4)
- 202009 (5)
- 202008 (6)
- 202007 (4)
- 202006 (4)
- 202005 (4)
- 202004 (7)
- 202003 (5)
- 202002 (6)
- 202001 (8)
- 201912 (6)
- 201911 (5)
- 201910 (3)
- 201909 (4)
- 201908 (10)
- 201907 (3)
- 201906 (6)
- 201905 (10)
- 201904 (3)
- 201903 (7)
- 201902 (8)
- 201901 (5)
- 201812 (7)
- 201811 (12)
- 201810 (7)
- 201809 (5)
- 201808 (10)
- 201807 (5)
- 201806 (19)
- 201805 (14)
- 201804 (11)
- 201803 (15)
- 201802 (4)
- 201801 (6)
- 201712 (4)
- 201711 (3)
- 201710 (11)
- 201709 (9)
- 201708 (15)
- 201707 (7)
- 201706 (4)
- 201705 (5)
- 201704 (6)
- 201703 (7)
- 201702 (6)
- 201701 (3)
- 201612 (3)
- 201611 (7)
- 201610 (7)
- 201609 (2)
- 201608 (8)
- 201607 (8)
- 201606 (7)
- 201605 (3)
- 201604 (4)
- 201603 (8)
- 201602 (3)
- 201601 (2)
- 201512 (3)
- 201511 (3)
- 201510 (4)
- 201509 (4)
- 201508 (8)
- 201507 (17)
- 201506 (2)
- 201505 (5)
- 201504 (9)
- 201503 (20)
- 201502 (7)
- 201501 (4)
- 201412 (5)
- 201411 (3)
- 201410 (2)
- 201409 (3)
- 201408 (3)
- 201407 (3)
- 201406 (12)
- 201405 (6)
- 201404 (7)
- 201403 (5)
- 201402 (12)
- 201401 (9)
- 201312 (6)
- 201311 (9)
- 201310 (8)
- 201309 (6)
- 201308 (6)
- 201307 (6)
- 201306 (10)
- 201305 (10)
- 201304 (23)
- 201303 (17)
- 201302 (16)
- 201301 (5)
- 201212 (10)
- 201211 (4)
- 201210 (18)
- 201209 (4)
- 201208 (30)
- 201207 (7)
- 201206 (4)
- 201205 (6)
- 201204 (4)
- 201203 (4)
- 201202 (3)
- 201201 (3)
- 201112 (4)
- 201111 (7)
- 201110 (3)
- 201109 (9)
- 201108 (3)
- 201107 (7)
- 201106 (2)
- 201105 (11)
- 201104 (7)
- 201103 (14)
- 201102 (19)
- 201101 (27)
- 201012 (25)
- 201011 (70)
- 201010 (34)
- 201009 (30)
- 201008 (42)
- 201007 (44)
- 201006 (29)
- 201005 (37)
- 201004 (50)
- 201003 (44)
- 201002 (48)
- 201001 (38)
- 200912 (20)
- recent trackback
- others
-
- RSS2.0
- hosted by チカッパ!
- HEAVEN INSITE(本サイト)


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 | 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 | 121 | 122 | 123 | 124 | 125 | 126 | 127 | 128 | 129 | 130 | 131 | 132 | 133 | 134 | 135 | 136 | 137 | 138 | 139 | 140 | 141 | 142 | 143 | 144 | 145 | 146 | 147 | 148 | 149 | 150 | 151 | 152 | 153 | 154 | 155 | 156 | 157 | 158 | 159 | 160 | 161 | 162 | 163 | 164 | 165 | 166 | 167 | 168 | 169 | 170 | 171 | 172 | 173 | 174 | 175 | 176 | 177 | 178 | 179 | 180 | 181 | 182 | 183 | 184 | 185 | 186 | 187 | 188 | 189 | 190 | 191 | 192 | 193 | 194 | 195 | 196 | 197 | 198 | 199 | 200 | 201 | 202 | 203 | 204 | 205 | 206 | 207 | 208 | 209 | 210 | 211 | 212 | 213 | 214 | 215 | 216 | 217 | 218 | 219 | 220 | 221 | 222 | 223 | 224 | 225 | 226 | 227 | 228 | 229 | 230 | 231 | 232 | 233 | 234 | 235 | 236 | 237 | 238 | 239 | 240 | 241 | 242 | 243 | 244 | 245 | 246 | 247 | 248 | 249 | 250 | 251 | 252 | 253 | 254 | 255 | 256 | 257 | 258 | 259 | 260 | 261 | 262 | 263 | 264 | 265 | 266 | 267 | 268 | 269 | 270 | 271 | 272 | 273 | 274 | 275 | 276 | 277 | 278 | 279 | 280 | 281 | 282 | 283 | 284 | 285 | 286 | 287 | 288 | 289 | 290 | 291 | 292 | 293 | 294 | 295 | 296 | 297 | 298 | 299 | 300 | 301 | 302 | 303 | 304 | 305 | 306 | 307 | 308 | 309 | 310 | 311 | 312 | 313 | 314 | 315 | 316 | 317 | 318 | 319 | 320 | 321 | 322 | 323 | 324 | 325 | 326 | 327 | 328 | 329 | 330 | 331 | 332 | 333 | 334 | 335 | 336 | 337 | 338 | 339 | 340 | 341 | 342 | 343 | 344 | 345 | 346 | 347 | 348 | 349 | 350 | 351 | 352 | 353 | 354 | 355 | 356