ある程度勝ったらすぐに帰宅が功を奏し、再び預けメダルが15万枚を超え、またまたプレミアムチャンスに挑戦してみました。
まず、判ったことは、プレミアムチャンスは出現する時間が決まっているということ。昨夜は合計で4回挑戦したのですが、7時、8時、9時、10時と00分前後に出てきたので、ほぼ確定。
ミリオンジャックポットと違って、時間が決まっているのならわけないわ!ヌハハハハハハ!!!と、7時の挑戦で20000枚マックスベットで回したら・・・
たった3分で20000枚が消滅しました。
その後、10時まで頑張ったのですが、プレミアムチャンス中セブンラッシュが来ることは一度もなかった・・・15万枚がまたまた12万枚に(´;ω;`)
なんじゃこりゃ、この前の悲劇といい、いつも12万枚にリセットされるぞ!シーシュポスの神話か。
つーか、これ、タイムセールの心理を利用した詐欺行為だと思う。こんなこと、社会的に許されるのか?
しかも、ダブルアップでは、ディーラーはトリプルバーとか7ばかり引いて、こっちはみかんしか出ないしね。本当に、露骨な八百長設定であったよ・・・
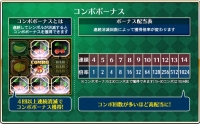
あれだな、プレミアムチャンスって、客にとってチャンスじゃなくて、店にとってのチャンスだろ。3分でメダルを2万枚も返却してもらえたわけだからな。
くそがーーー!!二度とやるかい!!!!!(500枚ベットでは)
以下は、2万枚の損失を取り戻そうとあがいて、さらに1万枚減った男の悲劇。※1000枚代は割愛しました。








確定音が2回続いて9000枚に。3度目はどうせみかんにされるなと諦めた。

このお姉さんの服、よく見てみるとスリットがめちゃくちゃエロいことが判明。
いや~ビデスロって本当に恐ろしいものですね~それではまた!(C)マイク水野
追記
翌日もちょっとだけ挑戦。つーか、時間帯関係なく、自分がログインしたらいきなりプレミアムチャンス出てきたし(30分代に出てきた)。すっかりカモにされてるな。




二度と破滅するのはゴメンだぜと、25~50ベットで手堅くゆっくり回しました。もちろん、セブンラッシュどころか、フリーゲームも入らない、安定の詐欺。※自分どころか誰も獲得してなかったし。もはやチャンスどころか、通常時よりも硬い。
ちなみに、他のプレーヤーさんの打ち方を見学してたんだけど、やはり、フィーチャーシリーズって、ハイベットしようがダブルアップ叩かないと増えないっぽいな。危ない橋を渡ることを強要する修羅のゲームやで・・・

いろんな意味で終了。

プッシャーは2000枚あれば一日中遊べるな。なんて健全なんだ・・・