フォーチュントリニティ4の正式稼動は来年の2月だそうです。え・・・もうすぐじゃん・・・いいよ、変わらなくて・・・
ロケテストをやった人の情報では、やはりジャックポットの獲得枚数がインフレを起こした結果、スロットが何十分も当たらなかったり(天井がなくなったという噂は本当だったのか)、オーブも全然払い出されなかったりと、基本的な内部設定はなかなか厳しく、2回ほどジャックポットを出してもメダルは大きく減っちゃうらしい。
最近のコナミのメダルゲームって全部このパターンだからなあ・・・嫌な予感してたんだよな。ジャックポット獲得枚数の期待値が大きくなっても、ゲーセン運営上、ペイアウトは据え置きなんだから、どっかにしわ寄せが来て、極端に回収するに決まってるんだから。
それに、FT4のロケテスト、すごい二転三転というか、めちゃくちゃ変更を繰り返しているけど、大丈夫なのかって不安になるよな。
FT3からのバージョンアップが間に合ってなかったところの追加じゃなくて、変更点をさらに変更しているからね。やっぱりロケテ参加者からのクレームが多かったんだろうな。
特によくわからないのが、ウンディーネジャックポットの抽選BGMの変更・・・の変更。曲をコロコロ差し替えるってあまり聞いたことないぞ。
倍率抽選のBGMは確かに最初のがかっこよかったから、1倍抽選曲に差し替えられたのが意味がわからなかったんだけど、結局元に戻ったっぽい。
しかし、その際に1倍抽選曲を新たに作ってしまったため(これがなぜかギターであまりかっこよくない)、旧1倍抽選曲の帰る場所がなくなり、今度はコイツがお蔵入りになってしまった。
あと、当初の抽選曲で一番かっこよかった2倍抽選曲(風を感じさせる綺麗な曲で、これが4倍でもいいと思ったくらい)も、いつの間にかいなくなってました。
で、当初4倍の抽選曲が、倍率変更ができることになって追加された3倍のテーマに、4倍のテーマは新曲に・・・や・・・ややこしい・・・!
もっと自分に自信を持てよ作曲陣(そして差し替えた曲の方がだいたい前より劣るのが切ない)。
ちなみに、今回のロケテから未公開だったライデンジャックポットとウンディーネジャックポットの演出が追加され(ダイビングスーツに着替えずに海底の遺跡に潜る親子・・・)、それに伴い公式サイトでも3精霊のビジュアルが公開されました。
ライデンジャックポットの曲は正直ちょっとかっこいいな。悔しいけど。電気だから、日本の雅楽をエレキギターで弾くっていう発想は出てきそうで出てこないわ。で、ウンディーネの方はあれだね、姫神だね。
それと、今回は至宝祭でお祭りだから、基本的に精霊も踊るのね。ライデン(雷神?)は神社で狂言、ウンディーネは地中海でクラシックバレエ(これも衝撃的!)、そしてイフリートは・・・空手?いや、こういう格闘技が中東にもあるのか?(イフリートはイスラームの魔人)
つーか、お前だけデザインが前作の大地神とかぶってるぞ。このゲームの世界だと炎属性はウシになるのだろうか。
あと、フリオやサニーたちの近況もわかります。サニーちゃんはやっぱりあれだね、サニー’sクッキングリターンズっていうリーチ演出は絶対作ったほうがいいね。
あと、今回はオーブくんが増殖したのか、友だちをたくさん連れてきたのか、まあどちらにしろ迷惑な話だけど、フォーチュンオーブのように仲間たちがかなり増えた。
なんと、フォーチュンオーブで、ひろしの前に立ちはだかったブラックオーブくんも再登場するらしい。
前3部作のフリオパパママやトレイシー、フェニックスやジャイアント、三神獣などのキャラクターを一新する代わりに、さらに昔のフォーチュンオーブのキャラを持ってくるのは確かにアリかもな。ならば、ひろしやキャサリンや博士もぜひ出して欲しいけどな。
ま、まあ、アップデート別に望んでないけどな。
フォーチュントリニティ3正気に戻る
2020-12-13 10:06:26 (5 years ago)
-
カテゴリタグ:
- ゲーム

約一ヶ月半、地獄の設定だったフォーチュントリニティ3ですが、とうとう一昨日あたりに設定を変更してくれたらしく、露骨に大放出するようになりました。
かつては上の写真のように、さんざみんなのメダルを強奪しておきながら(15万枚以上吸い込むのは当たり前)、3日か4日に一度だけ1~2倍で吐き出していたオーシャンジャックポットが昨日は連発!※内4倍が2回!



私もオーシャンは逃したものの(本当に相性悪いな)、グラウンドとワールドの計3回が出せて、メダルも久々に増えました。
そもそも、確変でもメダルが減っていくゲームなんだから、これくらいじゃないとやってて楽しくないよな。本当に11月からのフォーチュントリニティはひどかったもの。お客さんも誰もやってなかったしね。さすがに年末イベントに向けて設定を緩めたんだろうな。
極悪設定と言ったらFT3以上にひどかったカラコロッタも昨日から設定が大きくゆるくなって、久々の賑わいを見せていました。あれも5球とかでアウト連発してて、誰も寄り付かなくなってたからな・・・
さらに、設定が改善されたのはプッシャーだけじゃなく・・・







スロットキター!!なんと1日で14000枚も増えました。これはスロット史上過去最高かもしれん・・・セブンラッシュの破壊力をついに実感・・・!
あと、長いことキャリーオーバーで忘れ去られていた、こいつも成仏させてやった。こういうふうにハマっちゃっている時はどうせ1ラインで出るだろと、挑戦したら案の定です。

しかし、唯一鉄壁の守りを見せるモンスターがいた・・・!

確変が続いても・・・

女神が降臨しても・・・

確率5分の1というスーパーチャンスが来ても・・・
とにかくジャックポットが出ない。
そんな、高額を狙っているわけじゃないんだよ。たった一回くらい出してやってもいいだろって言ってんだよ。つーかさ、まずファンタジックチャンスがムズすぎるんだよ。※10球のボールを、赤か青のすべてのポケット(各5箇所)にボールを入れる。
あれってルール的にはアニマロッタのジャックポットチャンスだからね?つまり、予選どころの難易度じゃないんだよ。ジャックポットを狙うゲームの難易度なんだよ。
よく、おじいさんが何てことなくジャックポットとってるけど、自分には出せる気がしないもんな。777が来ても出ないし。なんか、出る台とかがあるのかな。

絵は可愛いんだけどね。

絶対5枚以上あるだろ!
R2年度警視庁事務採用試験について
2020-12-05 22:41:36 (5 years ago)
-
カテゴリタグ:
- 資格試験
なんか、やろうやろうと思い、今さらになってしまったやつ。今月はいよいよ年内最後の月なので、もう、いい加減、大地神(ウシ)を描かねば・・・
全体的な感想
制限時間は2時間だが、その分、問題の難易度は国家公務員試験よりも数倍高い。
※ガチンコでやって38点でした(英語が尾を引いた)。
文章理解は抽象的な哲学についての文章が多く、また英文読解の問題数も多い。
極めつけは、資料解釈のボリュームがとにかく多い。特に、前年度比(%)のグラフなどは、最終的に割合が向上しても、最初で激減していたら、結局は元の水準までに回復していなかったりするので、こういった資料の読み取り方を事前に学習しておくとよいでしょう。
また、数的処理の出題数がやや多い分、自然科学は割とあっさりだが(地学だけ例外)、社会科学や時事問題については、警察ならではというか、司法制度や犯罪につながりそうな社会問題などが選ばれている印象があり、ニュースはチェックしておいた方がいい。
データ
全45題 時間は120分
試験問題持ち帰り可能。
星の数は難易度。
☆:易しい。小中学生レベル。
☆☆:普通。高校生レベル。
☆☆☆:難しい。大学入試~大学生レベル。
文章理解
1.内容把握☆
アメリカの図書館のデータベースの特徴(多様な記事索引)や検索文化について。
大変易しい。
2.内容把握☆
茶の精神が茶室の中だけに限定されていて、茶事と日々の暮らしが分断されている状況を嘆いた、柳宗悦の文章。ツイッターでこういうことをうそぶくオタクは割といる。
すこし文章が長いが、ようは「真の茶人とはこうあるべきだ」的なめんどくさいことを言っているだけなので、論点は明確で易しい。
3.文章整序☆☆
5つの文章のパーツを順番通りに並び替える。
文章が哲学(カントやフッサールなどの知覚・認識論)なので、内容理解がちょっと難しい。
ただし、論理展開が不自然な選択肢が多いので、内容を理解できずとも消去法で正解できる。
※B→Dの順番になっている選択肢が一つしかない。
4.空欄補充☆☆☆
警視庁事務に必要な教養なのかわからないが、こちらも哲学。しかもデュルケム。
これは、どの用語を入れても何となく意味が成立するので、正直かなり難しい(「興奮にのぼせる」で決めるしかない)。
デュルケムは、社会は個人レベルに還元できない(心理学でいえばゲシュタルト学派)と考えていたので、そういった予備知識があると読解しやすいが、たぶん高卒の受験生デュルケムすら知らない。
5~8.英語
英語読めないので、難易度が見当つかないのが悲しい。
判断推理
9.数量関係☆
中学校の連立方程式で解ける文章問題。
3問のうち2問以上が正解した生徒の人数ということは、2問正解者と3問全問正解者の合計人数であることに注意。
10.組み合わせ☆☆
限られた数の紙幣と通貨で、ある金額を支払う場合の組み合わせは何通りあるか、みたいな中二の数学の単元にありそうな問題。
わりと100円と50円の小銭が多いが、これをすべて使っても100円×6+50円×8=1000円で、条件の2100円に100円足りなかったりするので、パターンはかなり絞り込める。
11.順序関係☆
これはかなり簡単。国語力があれば、順序はすべて確定する。
持参したお土産で、クッキーかぶりをしている人物が二人いるが、それしか条件が成り立たないので、そういうこともあるのだろう。
意味が分からないと思うので、問題を置いておきます。
次のヒントから、A~Dの4人の到着順序、お土産、交通手段を考えなさい。
・Aは、徒歩で到着した人の前に、ケーキを持って到着した。
・CはAと同じ交通手段で、Dの後に到着した。
・ケーキを持ってきた人は最後に到着した。
・ゼリーを持ってきた人は自転車で到着した。
・バスで到着した人は、クッキーを持って最初に到着した。
・2番目に到着した人は自転車で到着した。
数的処理
12.確率☆☆
4個のサイコロを同時に投げるとき、2個以上のサイコロが同じ目を出す確率はいくつかという問題。これは逆に、全部バラバラの目が出る確率(余事象)を求めた方が圧倒的に簡単。
13.幾何学☆
等間隔に点が並んでおり、点をつないでできる二等辺三角形はいくつできるかという問題。
そしてあまり二等辺三角形ができないので、瞬殺できます。
14.割合☆☆
方程式の文章問題。
問題文は減少前ではなく、減少後の%なので、逆算してやる必要がある。
各列車からは同じ人数の乗客が下車していることから一次方程式で行けます。
15.比の計算☆☆
収容数が異なる大中小のバスが全部で15台あり(収容人数比は大:中:小=7:4:3)、中型と小型のバスの台数を3倍にすると、収容数は2倍になりました。では、もともと所有していたバスはそれぞれ何台でしょうか?という、問題のアイディア的にはめちゃくちゃ難しい問題もつくれそうなポテンシャルを秘めているが、まさかのあてずっぽう(とりあえず5台ずつでいいか)できれいに解けてしまう。
前にも言ったように、公務員試験は一問あたり2~3分で解けるように作ってあると思われるので、こういう問題も見かけ倒しだったりする。
16.面積比☆
中学校3年生の方がもっと難しいのを解いてます。難易度にムラがあるのが公務員試験の特徴だよな。こういう雑魚キャラもあるわけだし。
17.角度☆
中学校2年生のが(以下略)多角形の内角の和さえ理解していれば瞬殺。
18.階差数列☆☆
式を作って一般化すると高校レベルだが(※最終的な公差が2の階差数列が出てくるため)、規則性が単純なため、ひたすら数列を進めていけば倒せてしまう。
資料解釈
問題数がかなり多い。そしてかなりやりごたえあり。
19.表☆☆
表自体は易しいが、選択肢が正しいのかいちいち計算をしてチェックするのが面倒(「平成27年に対する平成29年の比率は1.2を上回っている」という選択肢があるが、実際に計算すると1.09で若干少ないなど)。
電卓可でもいいと思う。
20.割合つき棒グラフ☆☆
19と同様、きわどい選択肢があるので、実際に計算が必要。
対前年増加率などの算出は桁が多いとかなりめんどうくさいし。
21.折れ線グラフ☆☆☆
グラフの縦軸(%)は、あくまでも“前年”からの増加比なので、プラスに転じたからと言って最初の数値から増加したとは限らない。
22.割合☆
これはけっこう易しい。
23.指数☆☆☆
グラフの下部にひっそりと書かれている(注)の部分をしっかり読まないと絶対解けない問題。「指数は平成25年を基準にしました」、とあるのでこれを踏まえる。
判断推理
また出てくる。空間把握能力やアニメーションをシミュレーションする能力が問われる。こういうのって男性の方が強いって話もあるけど、どうなんだろう。地図が読めない女とか本あったよな。
24.平面図形☆
二つの方眼紙を重ねて、着色されたマスが重なる数は最大いくつ?というもの。
選択肢が限られているので選びやすい。
25.平面図形☆
次の図形にはいくつの三角形が含まれますか?というベタな奴。
26.立体図形☆
150個の立方体が積まれていて、色がついた立方体はいくつになるか考える。
得意な人は得意なやつ。
27.平面図形の回転☆☆
毎回出てくる、公務員試験が超好きなやつ。
元の位置まで戻ってくるために必要な回転数を求める。
円周に直線(正三角形の辺)はどんな場合でも90度でしか接することができないため、円周の長さ分だけ移動することになる。なので、円周を切り開いて直線に変えて、三角形を転がしても大丈夫。すると、正三角形の一辺がπcm、円周の長さが6πcmなので1.5回転となる。
※三角形の一片の長さがπというところでちょっと怪しいと気付けるかを、警視庁は問うているのかも。
28.平面図形の回転と軌跡☆
図形の回転おかわり。
こちらでは直線状を転がる半円の中心点の軌跡を求める。
半円が曲面を下に向けてごろごろ転がっていくときの移動距離は、半円の円周の長さに等しく、さらに中心点の位置は変わりません(回転軸にあるため)。難しいのはそこだけかな。
教養問題
どこに含めばいいのかわからない、ノンセクション的な問題が3題ありました。
29.栄養学☆☆
栄養素に関する問題。まさかの家庭科。
①ちょっとマニアックだが、そば粉にはグルテンはない。
②ニンジンやホウレンソウはビタミンAに変化するカロテンを含み、緑黄色野菜と呼ばれるのは本当。これが正解。
③肉は部位によって成分は変わる。ヒレとロースでも結構違うし。
④無機質は体を作る栄養素ではない。トランスフォーマーか。
⑤水溶性ビタミンはC、B群。バターにビタミンAが入っているのは本当。
30.時事問題☆☆
まさかのマイナンバー。警察だから、詐欺や犯罪につながりかねないここら辺の知識は問われるってわけか。
①マイナンバーは15桁ではなく12桁。
②社会保障、税及び災害対策などで、複数の機関に存在する個人情報を同一人物の情報であることを確認するために活用される。正しい。
③マイナンバーカードの交付申請は、郵便、パソコン、スマホのみ・・・ではない。
なんと、証明写真機でも行ける。https://www.kojinbango-card.go.jp/kofushinse/
④マイナポイント事業は2019年ではなく2020年の9月に開始。
⑤来年の21年3月から、マイナカードは健康保険証として使用できるようになるが、現在は不可能。ウソみたいだけど、運転免許証との一体化も予定されており、菅政権は26年度をめどに考えているという。
31.情報工学☆
まさかの情報通信技術。警察だから、サイバー犯罪につながり(略)
コンピュータも10進法、OSは更新しない方がいい、音楽はネットでダウンロードできるようになったがCDの生産は増えているなど、頓珍漢な選択肢が多いため、正解を選ぶのはかなり簡単。
人文科学
32.日本史☆
安土桃山時代に関する記述として正しいものを選ぶ問題だが、5つ中3つが江戸時代の記述とのキメラなので、事実上の2択になる。そしてあとひとつが、千利休が浄瑠璃をやったという、もう、どう考えても違和感のあるものなので、楽勝でしょう。
33.日本史☆
こちらは明治時代。五箇条の御誓文が国家について、五榜の掲示が民衆についての内容というところはしっかり確認。易しい。
34.東洋史☆☆
イスラム世界の王朝と最盛期の王様の神経衰弱クイズ。
ウマイヤ朝、アッバース朝、セルジューク朝、オスマントルコあたりを抑えれば大丈夫。
①ウマイヤ朝はアラブ人至上主義。ムアーウィアが開いている。スレイマン1世はオスマントルコが最盛期の王様。時代がぜんっぜん違う。
②アッバース朝の最盛期の王はハールーン=アッラシードで正しい。ちなみに、同じく文教政策を重視したカール大帝と交流があった。
③ファーティマ朝がアフリカ、後ウマイヤ朝がイベリアなので、逆。
④ブワイフ朝を滅ぼしてセルジューク朝。
⑤サラディンが興したのはアイユーブ朝。その後、アイユーブ朝がマムルーク朝になる。
35.西洋史☆
まさかのニューディール政策一点突破。
フランクリンの方のルーズベルトがテネシー川を開発(TVAという公社を設立)した。
36.自然地理学☆
日本の気候。日本付近の気団を位置関係と特徴をおさえれば、危なげなく答えられる。
37.自然地理学☆
世界の気候帯と植生。
①ステップの土壌は肥沃。正解。
②サバナは温帯ではなく熱帯。
③タイガは広葉樹ではなく針葉樹。
④森林限界を超えたツンドラに高木は存在しない。
⑤熱帯にある草原はサバナ。プレーリーは北米の温帯草原のことで、南米ではパンパという。
社会科学
38.政治学☆☆☆
日本の国会について。①と⑤でかなり迷う。
①参議院の緊急集会は内閣の求めによって召集。細かいけれど内閣総理大臣ではない。
②衆議院解散後は臨時国会ではなく特別国会。
③衆議院の再可決は、出席議員の2/3の賛成。
④憲法改正案は、出席議員ではなく総議員の2/3の特別多数決が必要。
⑤条約締結の承認については、衆議院の議決が優越される。
39.政治学☆
裁判制度について。
裁判員制度は民事事件ではなく刑事事件を対象にしているということを知っていれば簡単。
40.経済学☆☆
国際収支について。
IMFの国際収支表の内訳をしっかりと覚える。
また、日本のサービス収支は赤字ということも重要。
41.経済学☆☆
財政の役割について。
財政投融資などややマニアック。
ビルトインスタビライザーと、フィスカルポリシーとポリシーミックスをごっちゃにしない。ごっちゃになるけど。
自然科学
42.物理学☆☆
自由落下の問題。
ただ小石が落下するだけ。とてつもなく簡単。
43.化学☆
気体の収集方法。中学校1年生レベル。
塩化水素の気体は空気(ほぼ窒素)より重い。
44.生物学☆
やはり出ました、光合成(同化)と呼吸(異化)。
基礎レベルの知識があればOKです。
45.地学☆☆☆
なんと地球の熱収支!
まさか、こんな内容が出ると思わなかったので授業で割愛していたやつ。
突然内容が大学っぽいが、温室効果がなければ地球の平均気温は-18℃になってしまうという話はけっこう有名。でも普通は知らないだろうなあ。自分も群馬大学の気象学の授業で習ったもん。
全体的な感想
制限時間は2時間だが、その分、問題の難易度は国家公務員試験よりも数倍高い。
※ガチンコでやって38点でした(英語が尾を引いた)。
文章理解は抽象的な哲学についての文章が多く、また英文読解の問題数も多い。
極めつけは、資料解釈のボリュームがとにかく多い。特に、前年度比(%)のグラフなどは、最終的に割合が向上しても、最初で激減していたら、結局は元の水準までに回復していなかったりするので、こういった資料の読み取り方を事前に学習しておくとよいでしょう。
また、数的処理の出題数がやや多い分、自然科学は割とあっさりだが(地学だけ例外)、社会科学や時事問題については、警察ならではというか、司法制度や犯罪につながりそうな社会問題などが選ばれている印象があり、ニュースはチェックしておいた方がいい。
データ
全45題 時間は120分
試験問題持ち帰り可能。
星の数は難易度。
☆:易しい。小中学生レベル。
☆☆:普通。高校生レベル。
☆☆☆:難しい。大学入試~大学生レベル。
文章理解
1.内容把握☆
アメリカの図書館のデータベースの特徴(多様な記事索引)や検索文化について。
大変易しい。
2.内容把握☆
茶の精神が茶室の中だけに限定されていて、茶事と日々の暮らしが分断されている状況を嘆いた、柳宗悦の文章。ツイッターでこういうことをうそぶくオタクは割といる。
すこし文章が長いが、ようは「真の茶人とはこうあるべきだ」的なめんどくさいことを言っているだけなので、論点は明確で易しい。
3.文章整序☆☆
5つの文章のパーツを順番通りに並び替える。
文章が哲学(カントやフッサールなどの知覚・認識論)なので、内容理解がちょっと難しい。
ただし、論理展開が不自然な選択肢が多いので、内容を理解できずとも消去法で正解できる。
※B→Dの順番になっている選択肢が一つしかない。
4.空欄補充☆☆☆
警視庁事務に必要な教養なのかわからないが、こちらも哲学。しかもデュルケム。
これは、どの用語を入れても何となく意味が成立するので、正直かなり難しい(「興奮にのぼせる」で決めるしかない)。
デュルケムは、社会は個人レベルに還元できない(心理学でいえばゲシュタルト学派)と考えていたので、そういった予備知識があると読解しやすいが、たぶん高卒の受験生デュルケムすら知らない。
5~8.英語
英語読めないので、難易度が見当つかないのが悲しい。
判断推理
9.数量関係☆
中学校の連立方程式で解ける文章問題。
3問のうち2問以上が正解した生徒の人数ということは、2問正解者と3問全問正解者の合計人数であることに注意。
10.組み合わせ☆☆
限られた数の紙幣と通貨で、ある金額を支払う場合の組み合わせは何通りあるか、みたいな中二の数学の単元にありそうな問題。
わりと100円と50円の小銭が多いが、これをすべて使っても100円×6+50円×8=1000円で、条件の2100円に100円足りなかったりするので、パターンはかなり絞り込める。
11.順序関係☆
これはかなり簡単。国語力があれば、順序はすべて確定する。
持参したお土産で、クッキーかぶりをしている人物が二人いるが、それしか条件が成り立たないので、そういうこともあるのだろう。
意味が分からないと思うので、問題を置いておきます。
次のヒントから、A~Dの4人の到着順序、お土産、交通手段を考えなさい。
・Aは、徒歩で到着した人の前に、ケーキを持って到着した。
・CはAと同じ交通手段で、Dの後に到着した。
・ケーキを持ってきた人は最後に到着した。
・ゼリーを持ってきた人は自転車で到着した。
・バスで到着した人は、クッキーを持って最初に到着した。
・2番目に到着した人は自転車で到着した。
数的処理
12.確率☆☆
4個のサイコロを同時に投げるとき、2個以上のサイコロが同じ目を出す確率はいくつかという問題。これは逆に、全部バラバラの目が出る確率(余事象)を求めた方が圧倒的に簡単。
13.幾何学☆
等間隔に点が並んでおり、点をつないでできる二等辺三角形はいくつできるかという問題。
そしてあまり二等辺三角形ができないので、瞬殺できます。
14.割合☆☆
方程式の文章問題。
問題文は減少前ではなく、減少後の%なので、逆算してやる必要がある。
各列車からは同じ人数の乗客が下車していることから一次方程式で行けます。
15.比の計算☆☆
収容数が異なる大中小のバスが全部で15台あり(収容人数比は大:中:小=7:4:3)、中型と小型のバスの台数を3倍にすると、収容数は2倍になりました。では、もともと所有していたバスはそれぞれ何台でしょうか?という、問題のアイディア的にはめちゃくちゃ難しい問題もつくれそうなポテンシャルを秘めているが、まさかのあてずっぽう(とりあえず5台ずつでいいか)できれいに解けてしまう。
前にも言ったように、公務員試験は一問あたり2~3分で解けるように作ってあると思われるので、こういう問題も見かけ倒しだったりする。
16.面積比☆
中学校3年生の方がもっと難しいのを解いてます。難易度にムラがあるのが公務員試験の特徴だよな。こういう雑魚キャラもあるわけだし。
17.角度☆
中学校2年生のが(以下略)多角形の内角の和さえ理解していれば瞬殺。
18.階差数列☆☆
式を作って一般化すると高校レベルだが(※最終的な公差が2の階差数列が出てくるため)、規則性が単純なため、ひたすら数列を進めていけば倒せてしまう。
資料解釈
問題数がかなり多い。そしてかなりやりごたえあり。
19.表☆☆
表自体は易しいが、選択肢が正しいのかいちいち計算をしてチェックするのが面倒(「平成27年に対する平成29年の比率は1.2を上回っている」という選択肢があるが、実際に計算すると1.09で若干少ないなど)。
電卓可でもいいと思う。
20.割合つき棒グラフ☆☆
19と同様、きわどい選択肢があるので、実際に計算が必要。
対前年増加率などの算出は桁が多いとかなりめんどうくさいし。
21.折れ線グラフ☆☆☆
グラフの縦軸(%)は、あくまでも“前年”からの増加比なので、プラスに転じたからと言って最初の数値から増加したとは限らない。
22.割合☆
これはけっこう易しい。
23.指数☆☆☆
グラフの下部にひっそりと書かれている(注)の部分をしっかり読まないと絶対解けない問題。「指数は平成25年を基準にしました」、とあるのでこれを踏まえる。
判断推理
また出てくる。空間把握能力やアニメーションをシミュレーションする能力が問われる。こういうのって男性の方が強いって話もあるけど、どうなんだろう。地図が読めない女とか本あったよな。
24.平面図形☆
二つの方眼紙を重ねて、着色されたマスが重なる数は最大いくつ?というもの。
選択肢が限られているので選びやすい。
25.平面図形☆
次の図形にはいくつの三角形が含まれますか?というベタな奴。
26.立体図形☆
150個の立方体が積まれていて、色がついた立方体はいくつになるか考える。
得意な人は得意なやつ。
27.平面図形の回転☆☆
毎回出てくる、公務員試験が超好きなやつ。
元の位置まで戻ってくるために必要な回転数を求める。
円周に直線(正三角形の辺)はどんな場合でも90度でしか接することができないため、円周の長さ分だけ移動することになる。なので、円周を切り開いて直線に変えて、三角形を転がしても大丈夫。すると、正三角形の一辺がπcm、円周の長さが6πcmなので1.5回転となる。
※三角形の一片の長さがπというところでちょっと怪しいと気付けるかを、警視庁は問うているのかも。
28.平面図形の回転と軌跡☆
図形の回転おかわり。
こちらでは直線状を転がる半円の中心点の軌跡を求める。
半円が曲面を下に向けてごろごろ転がっていくときの移動距離は、半円の円周の長さに等しく、さらに中心点の位置は変わりません(回転軸にあるため)。難しいのはそこだけかな。
教養問題
どこに含めばいいのかわからない、ノンセクション的な問題が3題ありました。
29.栄養学☆☆
栄養素に関する問題。まさかの家庭科。
①ちょっとマニアックだが、そば粉にはグルテンはない。
②ニンジンやホウレンソウはビタミンAに変化するカロテンを含み、緑黄色野菜と呼ばれるのは本当。これが正解。
③肉は部位によって成分は変わる。ヒレとロースでも結構違うし。
④無機質は体を作る栄養素ではない。トランスフォーマーか。
⑤水溶性ビタミンはC、B群。バターにビタミンAが入っているのは本当。
30.時事問題☆☆
まさかのマイナンバー。警察だから、詐欺や犯罪につながりかねないここら辺の知識は問われるってわけか。
①マイナンバーは15桁ではなく12桁。
②社会保障、税及び災害対策などで、複数の機関に存在する個人情報を同一人物の情報であることを確認するために活用される。正しい。
③マイナンバーカードの交付申請は、郵便、パソコン、スマホのみ・・・ではない。
なんと、証明写真機でも行ける。https://www.kojinbango-card.go.jp/kofushinse/
④マイナポイント事業は2019年ではなく2020年の9月に開始。
⑤来年の21年3月から、マイナカードは健康保険証として使用できるようになるが、現在は不可能。ウソみたいだけど、運転免許証との一体化も予定されており、菅政権は26年度をめどに考えているという。
31.情報工学☆
まさかの情報通信技術。警察だから、サイバー犯罪につながり(略)
コンピュータも10進法、OSは更新しない方がいい、音楽はネットでダウンロードできるようになったがCDの生産は増えているなど、頓珍漢な選択肢が多いため、正解を選ぶのはかなり簡単。
人文科学
32.日本史☆
安土桃山時代に関する記述として正しいものを選ぶ問題だが、5つ中3つが江戸時代の記述とのキメラなので、事実上の2択になる。そしてあとひとつが、千利休が浄瑠璃をやったという、もう、どう考えても違和感のあるものなので、楽勝でしょう。
33.日本史☆
こちらは明治時代。五箇条の御誓文が国家について、五榜の掲示が民衆についての内容というところはしっかり確認。易しい。
34.東洋史☆☆
イスラム世界の王朝と最盛期の王様の神経衰弱クイズ。
ウマイヤ朝、アッバース朝、セルジューク朝、オスマントルコあたりを抑えれば大丈夫。
①ウマイヤ朝はアラブ人至上主義。ムアーウィアが開いている。スレイマン1世はオスマントルコが最盛期の王様。時代がぜんっぜん違う。
②アッバース朝の最盛期の王はハールーン=アッラシードで正しい。ちなみに、同じく文教政策を重視したカール大帝と交流があった。
③ファーティマ朝がアフリカ、後ウマイヤ朝がイベリアなので、逆。
④ブワイフ朝を滅ぼしてセルジューク朝。
⑤サラディンが興したのはアイユーブ朝。その後、アイユーブ朝がマムルーク朝になる。
35.西洋史☆
まさかのニューディール政策一点突破。
フランクリンの方のルーズベルトがテネシー川を開発(TVAという公社を設立)した。
36.自然地理学☆
日本の気候。日本付近の気団を位置関係と特徴をおさえれば、危なげなく答えられる。
37.自然地理学☆
世界の気候帯と植生。
①ステップの土壌は肥沃。正解。
②サバナは温帯ではなく熱帯。
③タイガは広葉樹ではなく針葉樹。
④森林限界を超えたツンドラに高木は存在しない。
⑤熱帯にある草原はサバナ。プレーリーは北米の温帯草原のことで、南米ではパンパという。
社会科学
38.政治学☆☆☆
日本の国会について。①と⑤でかなり迷う。
①参議院の緊急集会は内閣の求めによって召集。細かいけれど内閣総理大臣ではない。
②衆議院解散後は臨時国会ではなく特別国会。
③衆議院の再可決は、出席議員の2/3の賛成。
④憲法改正案は、出席議員ではなく総議員の2/3の特別多数決が必要。
⑤条約締結の承認については、衆議院の議決が優越される。
39.政治学☆
裁判制度について。
裁判員制度は民事事件ではなく刑事事件を対象にしているということを知っていれば簡単。
40.経済学☆☆
国際収支について。
IMFの国際収支表の内訳をしっかりと覚える。
また、日本のサービス収支は赤字ということも重要。
41.経済学☆☆
財政の役割について。
財政投融資などややマニアック。
ビルトインスタビライザーと、フィスカルポリシーとポリシーミックスをごっちゃにしない。ごっちゃになるけど。
自然科学
42.物理学☆☆
自由落下の問題。
ただ小石が落下するだけ。とてつもなく簡単。
43.化学☆
気体の収集方法。中学校1年生レベル。
塩化水素の気体は空気(ほぼ窒素)より重い。
44.生物学☆
やはり出ました、光合成(同化)と呼吸(異化)。
基礎レベルの知識があればOKです。
45.地学☆☆☆
なんと地球の熱収支!
まさか、こんな内容が出ると思わなかったので授業で割愛していたやつ。
突然内容が大学っぽいが、温室効果がなければ地球の平均気温は-18℃になってしまうという話はけっこう有名。でも普通は知らないだろうなあ。自分も群馬大学の気象学の授業で習ったもん。
メダルゲーム大苦戦
2020-11-28 12:57:20 (5 years ago)
-
カテゴリタグ:
- ゲーム
13万枚の壁を破った翌日、目標を達成し満足した私は、トゥインクルドロップのフリーゲームでダブルアップなしで10000枚は超えるのか検証してみたくなり、結果あっさり30000枚飲まれるという、来るべくしてきた破滅を迎え、さらにプッシャーの設定も未だに悪く、10万枚前後をさまよっています。
つーか、ついにその本性を見せたな、フィーチャーワールド。設定を閉められちゃうとマシンデータも通用しねえわ・・・10000枚以上突っ込んでも、フリーゲーム全然出ないし、やっと出せたフリーゲームでも300枚くらいしか出ないもんな。鬼畜極まりない。
これなら、まだ、フィーチャープレミアムの方がコンスタントに返してくれるけど、この綱渡りもいつまで続くかわからないからなあ・・・


でも、こんなもんです。1000~1500枚の増加って程度。


私の生きがい、フォーチュントリニティは本当に出ない。あまりに出なさすぎて、誰もやらない→メダルを飲まない→もっと出ない→さらに誰もやらない・・・の悪循環が完成。
カラコロッタと共に無人の日々が続いています。どうしてこうなった??



大健闘したのはビー玉。確変が50回以上も続き、ジャックポットチャンスでも最終抽選に常時2球到達するという、甘甘設定で立て続けにジャックポット。この機種では驚異的の2000枚増加。

案の定、つまり申した。

最近面白くなってきたのが、フォーチュンオーブ3。メダルチャッカーが斜めのスリットになっていて、スロットストックを貯めるのが難しすぎて長いこと敬遠していたが、コツをつかむとあのスリットにメダルをはめるのが病みつきになるという。
ちなみに、このゲームをやるとオーブくんが固有名詞ではなく種族ということがわかる。リボンをつけたメスもいるし(上図参照)、ヒゲのある老齢の個体も確認。
したがって、スマッシュスタジアムのオーブくんは、別にフリオ親子を捨てたのではなく、別個体の可能性の方が高い気がしてきた。

プレステ初代くらいのグラフィックでかなり懐かしい。この時代のCGってけっこう好きなんだよな。デザーテッドアイランドとか。

フォーチュントリニティ1に受け継がれた演出。もちろん外すと膝から崩れます。

ひろしの運命やいかに!?

プッシャーゲームのジャックポット枚数を大きく増加し、業界に激震を与えたフォーチュンオーブのスーパージャックポット。オーシャンジャックポットのご先祖様だが、ジャックポットの確率は1/10でオーシャンより少し優しい(出たことないけど)。
つーか、スーパージャックポットでも同じフィールドオーブを用いるのね。上に持ち上げて、外周の観覧車で抽選ルーレットに送るのとか、すごいかっこいい。
て、ことで、今やメダルを大きく減らす可能性が高いスロットはほどほどに、今後はローリスクなレトロプッシャーを攻略していきます。
2年近く通っていて、一度もジャックポットを出したことがないのが、このフォーチュンオーブとファンタジックフィーバー3なので、こいつらがジャックポットを出すまで、ボクはメダルを入れるのをやめない!
あ、未攻略のスロットと言ったら、パイレーツ・ア・ゴーゴーなんだけど、昨日撤去されて、基盤が別の萌えスロットに変わってました・・・(´;ω;`)

9ベットで、数千枚ストレート負け。クソつまらねー。
追記

ブログを更新したその日の夜に奥さんとふらりと寄ったら、あっさり攻略することができました!これで残るはファンタジックフィーバー3のみだな。

めちゃくちゃ勢いよく払い出されるんだけど、メダルがウロコ状に重なっちゃって半分弱くらいしか落ちないようです(重い)。だいたい700枚増加ってところ。でも初の経験だったので超嬉しい。

スーパージャックポットを失敗しても300枚の払い出しだとセンターから出てくるのね。

もっとも怖いリーチ演出。ふ・・・普通に食われてるんだけど・・・逃げきれてヤッターじゃねーし。

人食い生物がいる地獄のオーブキングダムから脱出できたので、めでたしめでたし。
つーか、ついにその本性を見せたな、フィーチャーワールド。設定を閉められちゃうとマシンデータも通用しねえわ・・・10000枚以上突っ込んでも、フリーゲーム全然出ないし、やっと出せたフリーゲームでも300枚くらいしか出ないもんな。鬼畜極まりない。
これなら、まだ、フィーチャープレミアムの方がコンスタントに返してくれるけど、この綱渡りもいつまで続くかわからないからなあ・・・


でも、こんなもんです。1000~1500枚の増加って程度。


私の生きがい、フォーチュントリニティは本当に出ない。あまりに出なさすぎて、誰もやらない→メダルを飲まない→もっと出ない→さらに誰もやらない・・・の悪循環が完成。
カラコロッタと共に無人の日々が続いています。どうしてこうなった??



大健闘したのはビー玉。確変が50回以上も続き、ジャックポットチャンスでも最終抽選に常時2球到達するという、甘甘設定で立て続けにジャックポット。この機種では驚異的の2000枚増加。

案の定、つまり申した。

最近面白くなってきたのが、フォーチュンオーブ3。メダルチャッカーが斜めのスリットになっていて、スロットストックを貯めるのが難しすぎて長いこと敬遠していたが、コツをつかむとあのスリットにメダルをはめるのが病みつきになるという。
ちなみに、このゲームをやるとオーブくんが固有名詞ではなく種族ということがわかる。リボンをつけたメスもいるし(上図参照)、ヒゲのある老齢の個体も確認。
したがって、スマッシュスタジアムのオーブくんは、別にフリオ親子を捨てたのではなく、別個体の可能性の方が高い気がしてきた。

プレステ初代くらいのグラフィックでかなり懐かしい。この時代のCGってけっこう好きなんだよな。デザーテッドアイランドとか。

フォーチュントリニティ1に受け継がれた演出。もちろん外すと膝から崩れます。

ひろしの運命やいかに!?

プッシャーゲームのジャックポット枚数を大きく増加し、業界に激震を与えたフォーチュンオーブのスーパージャックポット。オーシャンジャックポットのご先祖様だが、ジャックポットの確率は1/10でオーシャンより少し優しい(出たことないけど)。
つーか、スーパージャックポットでも同じフィールドオーブを用いるのね。上に持ち上げて、外周の観覧車で抽選ルーレットに送るのとか、すごいかっこいい。
て、ことで、今やメダルを大きく減らす可能性が高いスロットはほどほどに、今後はローリスクなレトロプッシャーを攻略していきます。
2年近く通っていて、一度もジャックポットを出したことがないのが、このフォーチュンオーブとファンタジックフィーバー3なので、こいつらがジャックポットを出すまで、ボクはメダルを入れるのをやめない!
あ、未攻略のスロットと言ったら、パイレーツ・ア・ゴーゴーなんだけど、昨日撤去されて、基盤が別の萌えスロットに変わってました・・・(´;ω;`)

9ベットで、数千枚ストレート負け。クソつまらねー。
追記

ブログを更新したその日の夜に奥さんとふらりと寄ったら、あっさり攻略することができました!これで残るはファンタジックフィーバー3のみだな。

めちゃくちゃ勢いよく払い出されるんだけど、メダルがウロコ状に重なっちゃって半分弱くらいしか落ちないようです(重い)。だいたい700枚増加ってところ。でも初の経験だったので超嬉しい。

スーパージャックポットを失敗しても300枚の払い出しだとセンターから出てくるのね。

もっとも怖いリーチ演出。ふ・・・普通に食われてるんだけど・・・逃げきれてヤッターじゃねーし。

人食い生物がいる地獄のオーブキングダムから脱出できたので、めでたしめでたし。
13万枚の壁
2020-11-22 10:06:10 (5 years ago)
-
カテゴリタグ:
- ゲーム
今月はプッシャー機の設定が辛く、12万枚を超えてから12万5000枚近辺を一進一退でウロウロしている感じで2週間が過ぎた・・・
プッシャー機に見切りを付け、最近はじめた新しいスロットの遊びが、フィーチャープレミアムの各機種でマックス500枚ベットを一回だけやって、ダメならロシアンルーレットみたいにとなりの機種に移っていくっていうやつで、おそらくあの機種ってあのエリア全体でペイアウト設定してそうだから、どこかの機種で大きく帰ってくるだろうと。

で、この前はパイレーツアゴーゴーに飲まれたあと、隣のトゥインクルドロップジュークで早くも結構でかいのが出たから、わりと増やせることのほうが多いプレースタイルかな、と。まさか全台飲むっていうのはなかなかないだろうかな。仮にそれでも、500枚×6種類(パティシエッタ、パイレーツ、ジューク、フローズンタワー、ラッシュ、ジュエルクライマー)で3000枚の損失で済むしな。なんかスロットで感覚が麻痺して3000枚の重さが軽くなっている気はするけど。
だが、そんなフィーチャープレミアムシリーズの中で私が唯一惨敗し、大勝を一度もしたことがない強敵がいた・・・!
その名はジュエルクライマー!!!パニックパイレーツのフォーチュントリニティ版って感じなんだけど、まずフリーゲームが鬼ほど出ず、通常のスロットも何も当たらず、18ベットという安全な枚数で回していたのにも関わらず、何も起きずに2000枚マイナス。
最後の方でかろうじて出た待望のフリーゲームでさぞ爆発するのかと思いきや、まさかの0枚。称号「明日があるさ」獲得!・・・っていらねーよ!!!この仕打ちはあまりにもむごい。

今月初めて出た4倍オーシャンで増えたメダルの半分強がフリオのオヤジに飲まれました。おのれ、親子で連携プレーか、やるじゃねえか・・・
むごいと言ったら、最近のカラコロッタも本当に鬼畜で、あんなにいたハイベッターの常連さんがここ最近は一切寄り付かず、フォーチュントリニティ3同様、閑散としております。自分も399mでトーテムぐんぐんを崩壊させられて以来やっておりません。
てことで、最近の傾向。
フォーチュントリニティ3:危険度☆☆
基本的によくない。オーシャンは本当に出なくなった。2000枚まで貯まらないと最近は出さないイメージ。そしてそこまで貯めても4倍が出るとは限らない。というか出ないことのが多い。
基本的に確変が出ない台は、JPチャンスがいくら多くても入らないし、入ってもジャックポットは出ないのは定石と化しています。

赤のイベントでもこんなもん。イベントなのにそもそも誰もやってないしね。
スピンフィーバー3:危険度☆
あまりにやるゲームがないので、すごい久々にやったらビギナーズラックでなかなか出ないらしいゴールドジャックポット獲得(777からの移行)。これを出すとスタッフロールが流れるんだけど、撮影中カメラがフリーズしてしまいデータが死んだ(´;ω;`)
ただ、後半でI wanna kiss youがメドレーっぽく流れるのは熱い。もう二度と取れない気がするけど(そもそもこの機種あまりやらないから)、またチャンスがあったら今度は撮影を成功させてアーカイブに残したいです。

カラコロッタ:危険度☆☆☆☆☆
だいたい6~7球でアウトが続き、パーティタイムの可能性があるときは9球とかショップタイム直後の11球で終わることがあまりにも多い。あと4球目でアウトで復活チャンスで失敗、もしくは成功しても次の球でアウトとか。やってられるか。この設定で今後も行くなら、いっそ撤去してくれ。カラコロッタ勢の常連さんも来なくなったもんなあ。
G1ワールドクラシック:危険度☆☆☆
基本的に最近は本命中心のレース展開が多いです。ただし、自分がいなかった時にレースがかなり荒れたらしく、40000枚の配当が出たらしい。ロマンである。
最近は、その40000枚の常連さんと本命&大穴を別々に担当して、どっちかは来るだろうみたいな遊び方をしています。

トゥインクルドロップ:危険度☆☆☆
フィーチャーワールドはプレミアムと違ってマシンデータという大変ありがたい機能があり、過去の成績をふまえて、やるかどうかを考えられるので、すごい助かる。
常連さんいわく、フリーまでに回した回数の合計と、獲得配当の合計を割って、損失が大きいようならマックスベットでデスマッチをすると、フリーゲームで20000枚とか行くらしい。
つーか、フリーゲームが継続しやすいパニックパイレーツなら分かるけど、回数が事前に決まっているトゥインクルドロップのフリーゲームでダブルアップなしで20000枚はちょっと聞いたことがない。マジかよっていう。
私は、だいたい5000枚くらいのが出ちゃうとやめちゃうからなあ。ダブルアップも心臓に悪いしな。でも一度は、ダブルアップで10000枚を超えたい気はする。そんなチャンスは、このゲームって結構くるんだけど、チキってしまうのよ。そこに至るまでに5000枚くらい減ってるからw


パニックパイレーツ:危険度☆☆☆
こちらもマシンデータを踏まえてやれば惨敗はない。・・・今のところ。ただ、トゥインクルドロップと比べてフリーゲームの可能性が計り知れない分、はまってしまうと500回以上回してもフリーゲームが来ない時がある。そしてそのフリーゲームであまりにもしょぼい配当が出た場合は決して挫けてはいけない。さらに3000枚くらいおろして回し続ければ、きっと嬉しいことがおきます。フィーチャーワールドは波は荒いんだけど、ちゃんと反動が来るので、最悪半分位は取り返せます。
ジュエルクライマー:危険度☆☆☆☆☆
パニックパイレーツとルールが同じはずなのに、くそつまらねー。
パイレーツ・ア・ゴーゴー:危険度☆☆☆
ボスが強すぎる。勝てる日は来るのだろうか。いや、ない。
このゲームだけは、ダブルアップが良くも悪くもたたけないので、欲に目がくらんで大負けっていうのが原理的にありえない。
トゥインクルドロップラッシュ:危険度☆☆☆☆
マシンデータが参照できない分リスクは大きい。ただし、セブンラッシュという7の役が揃いやすいモードが神出鬼没に発生するので(だいたいバーなどでかい配当が来た場合でてくる)、ここにフリーゲームが加わると無限大の可能性を秘めていることがわかった。
自分も、この前はじめてフリーゲームが出て、青と赤の777がそろい、5900枚が出て、まあ、その時は一度でいいからセブンラッシュが見たかったってだけだったのでコレクトしちゃったんだけど、ああいうことはそうそう起きないと思われる。
トゥインクルドロップジューク:危険度☆☆☆☆
赤(絵柄変更サービス)よりも青(フリーゲームや7をリザーブエリアに突っ込んでくれる)のショータイムの方がいいです。ただし、このショーが始まるまでにステップを7も貯めなければいけないので、その頃には死んだ目をしてスロットを回していると思われる。
ある程度通常のフリーゲームで小当りしたらやめちゃったほうがいいな。
パティシエッタ&フローズンタワー:危険度☆☆☆☆☆
基本的に負ける。ただ個人的に相性がいいのはフローズンかな。でも一度、10000枚丸々飲まれたことあったしな。何回か100ベットで回してまったく兆候がなかったら撤退が賢明です。
内部がよかったら5回転くらいで「!!」とか出るからね。ちなみに「!!」が出ても爆弾だけとか、×1~2の配当とかだった場合、もう絶対にやめたほうがいい。
あと、二番目のタワーを攻略している人、パイレーツ・ア・ゴーゴーのボス撃破並みに見たことがない。
追記
この記事を書いた午後に、トゥインクルドロップとラッシュで7700枚増加し、13万枚の壁ついに撃破!

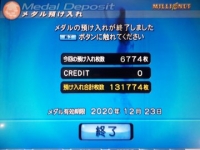
しかし、フォーチュントリニティは逆さに降っても出なかった・・・基本的にはメダルゲームってプッシャーのが好きなんだけど、あんなに長時間やって2000~3000枚の増加を目指すのがバカバカしくなるよな。
スロットだとそこそこツイてればオーシャンジャックポットの10000枚くらいのが5分であっさり出ちゃうからな。良くも悪くも、スロットはプッシャー的なサウナ感ないからな。
プッシャー機に見切りを付け、最近はじめた新しいスロットの遊びが、フィーチャープレミアムの各機種でマックス500枚ベットを一回だけやって、ダメならロシアンルーレットみたいにとなりの機種に移っていくっていうやつで、おそらくあの機種ってあのエリア全体でペイアウト設定してそうだから、どこかの機種で大きく帰ってくるだろうと。

で、この前はパイレーツアゴーゴーに飲まれたあと、隣のトゥインクルドロップジュークで早くも結構でかいのが出たから、わりと増やせることのほうが多いプレースタイルかな、と。まさか全台飲むっていうのはなかなかないだろうかな。仮にそれでも、500枚×6種類(パティシエッタ、パイレーツ、ジューク、フローズンタワー、ラッシュ、ジュエルクライマー)で3000枚の損失で済むしな。なんかスロットで感覚が麻痺して3000枚の重さが軽くなっている気はするけど。
だが、そんなフィーチャープレミアムシリーズの中で私が唯一惨敗し、大勝を一度もしたことがない強敵がいた・・・!
その名はジュエルクライマー!!!パニックパイレーツのフォーチュントリニティ版って感じなんだけど、まずフリーゲームが鬼ほど出ず、通常のスロットも何も当たらず、18ベットという安全な枚数で回していたのにも関わらず、何も起きずに2000枚マイナス。
最後の方でかろうじて出た待望のフリーゲームでさぞ爆発するのかと思いきや、まさかの0枚。称号「明日があるさ」獲得!・・・っていらねーよ!!!この仕打ちはあまりにもむごい。

今月初めて出た4倍オーシャンで増えたメダルの半分強がフリオのオヤジに飲まれました。おのれ、親子で連携プレーか、やるじゃねえか・・・
むごいと言ったら、最近のカラコロッタも本当に鬼畜で、あんなにいたハイベッターの常連さんがここ最近は一切寄り付かず、フォーチュントリニティ3同様、閑散としております。自分も399mでトーテムぐんぐんを崩壊させられて以来やっておりません。
てことで、最近の傾向。
フォーチュントリニティ3:危険度☆☆
基本的によくない。オーシャンは本当に出なくなった。2000枚まで貯まらないと最近は出さないイメージ。そしてそこまで貯めても4倍が出るとは限らない。というか出ないことのが多い。
基本的に確変が出ない台は、JPチャンスがいくら多くても入らないし、入ってもジャックポットは出ないのは定石と化しています。

赤のイベントでもこんなもん。イベントなのにそもそも誰もやってないしね。
スピンフィーバー3:危険度☆
あまりにやるゲームがないので、すごい久々にやったらビギナーズラックでなかなか出ないらしいゴールドジャックポット獲得(777からの移行)。これを出すとスタッフロールが流れるんだけど、撮影中カメラがフリーズしてしまいデータが死んだ(´;ω;`)
ただ、後半でI wanna kiss youがメドレーっぽく流れるのは熱い。もう二度と取れない気がするけど(そもそもこの機種あまりやらないから)、またチャンスがあったら今度は撮影を成功させてアーカイブに残したいです。

カラコロッタ:危険度☆☆☆☆☆
だいたい6~7球でアウトが続き、パーティタイムの可能性があるときは9球とかショップタイム直後の11球で終わることがあまりにも多い。あと4球目でアウトで復活チャンスで失敗、もしくは成功しても次の球でアウトとか。やってられるか。この設定で今後も行くなら、いっそ撤去してくれ。カラコロッタ勢の常連さんも来なくなったもんなあ。
G1ワールドクラシック:危険度☆☆☆
基本的に最近は本命中心のレース展開が多いです。ただし、自分がいなかった時にレースがかなり荒れたらしく、40000枚の配当が出たらしい。ロマンである。
最近は、その40000枚の常連さんと本命&大穴を別々に担当して、どっちかは来るだろうみたいな遊び方をしています。

トゥインクルドロップ:危険度☆☆☆
フィーチャーワールドはプレミアムと違ってマシンデータという大変ありがたい機能があり、過去の成績をふまえて、やるかどうかを考えられるので、すごい助かる。
常連さんいわく、フリーまでに回した回数の合計と、獲得配当の合計を割って、損失が大きいようならマックスベットでデスマッチをすると、フリーゲームで20000枚とか行くらしい。
つーか、フリーゲームが継続しやすいパニックパイレーツなら分かるけど、回数が事前に決まっているトゥインクルドロップのフリーゲームでダブルアップなしで20000枚はちょっと聞いたことがない。マジかよっていう。
私は、だいたい5000枚くらいのが出ちゃうとやめちゃうからなあ。ダブルアップも心臓に悪いしな。でも一度は、ダブルアップで10000枚を超えたい気はする。そんなチャンスは、このゲームって結構くるんだけど、チキってしまうのよ。そこに至るまでに5000枚くらい減ってるからw


パニックパイレーツ:危険度☆☆☆
こちらもマシンデータを踏まえてやれば惨敗はない。・・・今のところ。ただ、トゥインクルドロップと比べてフリーゲームの可能性が計り知れない分、はまってしまうと500回以上回してもフリーゲームが来ない時がある。そしてそのフリーゲームであまりにもしょぼい配当が出た場合は決して挫けてはいけない。さらに3000枚くらいおろして回し続ければ、きっと嬉しいことがおきます。フィーチャーワールドは波は荒いんだけど、ちゃんと反動が来るので、最悪半分位は取り返せます。
ジュエルクライマー:危険度☆☆☆☆☆
パニックパイレーツとルールが同じはずなのに、くそつまらねー。
パイレーツ・ア・ゴーゴー:危険度☆☆☆
ボスが強すぎる。勝てる日は来るのだろうか。いや、ない。
このゲームだけは、ダブルアップが良くも悪くもたたけないので、欲に目がくらんで大負けっていうのが原理的にありえない。
トゥインクルドロップラッシュ:危険度☆☆☆☆
マシンデータが参照できない分リスクは大きい。ただし、セブンラッシュという7の役が揃いやすいモードが神出鬼没に発生するので(だいたいバーなどでかい配当が来た場合でてくる)、ここにフリーゲームが加わると無限大の可能性を秘めていることがわかった。
自分も、この前はじめてフリーゲームが出て、青と赤の777がそろい、5900枚が出て、まあ、その時は一度でいいからセブンラッシュが見たかったってだけだったのでコレクトしちゃったんだけど、ああいうことはそうそう起きないと思われる。
トゥインクルドロップジューク:危険度☆☆☆☆
赤(絵柄変更サービス)よりも青(フリーゲームや7をリザーブエリアに突っ込んでくれる)のショータイムの方がいいです。ただし、このショーが始まるまでにステップを7も貯めなければいけないので、その頃には死んだ目をしてスロットを回していると思われる。
ある程度通常のフリーゲームで小当りしたらやめちゃったほうがいいな。
パティシエッタ&フローズンタワー:危険度☆☆☆☆☆
基本的に負ける。ただ個人的に相性がいいのはフローズンかな。でも一度、10000枚丸々飲まれたことあったしな。何回か100ベットで回してまったく兆候がなかったら撤退が賢明です。
内部がよかったら5回転くらいで「!!」とか出るからね。ちなみに「!!」が出ても爆弾だけとか、×1~2の配当とかだった場合、もう絶対にやめたほうがいい。
あと、二番目のタワーを攻略している人、パイレーツ・ア・ゴーゴーのボス撃破並みに見たことがない。
追記
この記事を書いた午後に、トゥインクルドロップとラッシュで7700枚増加し、13万枚の壁ついに撃破!


しかし、フォーチュントリニティは逆さに降っても出なかった・・・基本的にはメダルゲームってプッシャーのが好きなんだけど、あんなに長時間やって2000~3000枚の増加を目指すのがバカバカしくなるよな。
スロットだとそこそこツイてればオーシャンジャックポットの10000枚くらいのが5分であっさり出ちゃうからな。良くも悪くも、スロットはプッシャー的なサウナ感ないからな。
- Calendar
<< January 2026 >> Sun Mon Tue Wed Thu Fri Sat 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
- search this site.
- tags
-
- 漫画 (387)
- 脚本 (243)
- 映画 (235)
- 雑記 (163)
- ゲーム (156)
- 本 (116)
- 教育 (107)
- 生物学 (105)
- 科学 (93)
- 社会学 (81)
- 歴史 (72)
- テレビ (71)
- 芸術 (61)
- 政治 (50)
- 数学 (40)
- 進化論 (40)
- 資格試験 (38)
- 情報 (38)
- サイト・ブログ (37)
- 語学 (37)
- 映画論 (36)
- 物理学 (33)
- 哲学 (32)
- 恐竜 (29)
- 育児 (28)
- 文学 (26)
- 化学 (25)
- 論文 (22)
- PIXAR (22)
- 心理学 (18)
- 地学 (16)
- 気象学 (15)
- 地理学 (15)
- 技術 (13)
- 経済学 (12)
- 医学 (11)
- 玩具 (9)
- 司書 (8)
- 法律学 (7)
- 対談 (5)
- スポーツ (4)
- 映画の評価について (1)
- プロフィール (1)
- archives
-
- 202601 (2)
- 202512 (4)
- 202511 (15)
- 202510 (8)
- 202509 (5)
- 202508 (3)
- 202507 (3)
- 202506 (3)
- 202505 (1)
- 202504 (2)
- 202503 (2)
- 202502 (2)
- 202501 (1)
- 202412 (2)
- 202411 (6)
- 202410 (2)
- 202409 (4)
- 202408 (4)
- 202407 (7)
- 202406 (27)
- 202405 (11)
- 202404 (4)
- 202403 (23)
- 202402 (22)
- 202401 (15)
- 202312 (4)
- 202311 (7)
- 202310 (2)
- 202309 (8)
- 202308 (9)
- 202307 (8)
- 202306 (5)
- 202305 (15)
- 202304 (4)
- 202303 (4)
- 202302 (2)
- 202301 (4)
- 202212 (15)
- 202211 (7)
- 202210 (5)
- 202209 (4)
- 202208 (4)
- 202207 (7)
- 202206 (2)
- 202205 (5)
- 202204 (3)
- 202203 (2)
- 202202 (5)
- 202201 (6)
- 202112 (6)
- 202111 (4)
- 202110 (6)
- 202109 (7)
- 202108 (5)
- 202107 (8)
- 202106 (4)
- 202105 (8)
- 202104 (4)
- 202103 (6)
- 202102 (10)
- 202101 (3)
- 202012 (12)
- 202011 (3)
- 202010 (4)
- 202009 (5)
- 202008 (6)
- 202007 (4)
- 202006 (4)
- 202005 (4)
- 202004 (7)
- 202003 (5)
- 202002 (6)
- 202001 (8)
- 201912 (6)
- 201911 (5)
- 201910 (3)
- 201909 (4)
- 201908 (10)
- 201907 (3)
- 201906 (6)
- 201905 (10)
- 201904 (3)
- 201903 (7)
- 201902 (8)
- 201901 (5)
- 201812 (7)
- 201811 (12)
- 201810 (7)
- 201809 (5)
- 201808 (10)
- 201807 (5)
- 201806 (19)
- 201805 (14)
- 201804 (11)
- 201803 (15)
- 201802 (4)
- 201801 (6)
- 201712 (4)
- 201711 (3)
- 201710 (11)
- 201709 (9)
- 201708 (15)
- 201707 (7)
- 201706 (4)
- 201705 (5)
- 201704 (6)
- 201703 (7)
- 201702 (6)
- 201701 (3)
- 201612 (3)
- 201611 (7)
- 201610 (7)
- 201609 (2)
- 201608 (8)
- 201607 (8)
- 201606 (7)
- 201605 (3)
- 201604 (4)
- 201603 (8)
- 201602 (3)
- 201601 (2)
- 201512 (3)
- 201511 (3)
- 201510 (4)
- 201509 (4)
- 201508 (8)
- 201507 (17)
- 201506 (2)
- 201505 (5)
- 201504 (9)
- 201503 (20)
- 201502 (7)
- 201501 (4)
- 201412 (5)
- 201411 (3)
- 201410 (2)
- 201409 (3)
- 201408 (3)
- 201407 (3)
- 201406 (12)
- 201405 (6)
- 201404 (7)
- 201403 (5)
- 201402 (12)
- 201401 (9)
- 201312 (6)
- 201311 (9)
- 201310 (8)
- 201309 (6)
- 201308 (6)
- 201307 (6)
- 201306 (10)
- 201305 (10)
- 201304 (23)
- 201303 (17)
- 201302 (16)
- 201301 (5)
- 201212 (10)
- 201211 (4)
- 201210 (18)
- 201209 (4)
- 201208 (30)
- 201207 (7)
- 201206 (4)
- 201205 (6)
- 201204 (4)
- 201203 (4)
- 201202 (3)
- 201201 (3)
- 201112 (4)
- 201111 (7)
- 201110 (3)
- 201109 (9)
- 201108 (3)
- 201107 (7)
- 201106 (2)
- 201105 (11)
- 201104 (7)
- 201103 (14)
- 201102 (19)
- 201101 (27)
- 201012 (25)
- 201011 (70)
- 201010 (34)
- 201009 (30)
- 201008 (42)
- 201007 (44)
- 201006 (29)
- 201005 (37)
- 201004 (50)
- 201003 (44)
- 201002 (48)
- 201001 (38)
- 200912 (20)
- recent trackback
- others
-
- RSS2.0
- hosted by チカッパ!
- HEAVEN INSITE(本サイト)


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 | 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 | 121 | 122 | 123 | 124 | 125 | 126 | 127 | 128 | 129 | 130 | 131 | 132 | 133 | 134 | 135 | 136 | 137 | 138 | 139 | 140 | 141 | 142 | 143 | 144 | 145 | 146 | 147 | 148 | 149 | 150 | 151 | 152 | 153 | 154 | 155 | 156 | 157 | 158 | 159 | 160 | 161 | 162 | 163 | 164 | 165 | 166 | 167 | 168 | 169 | 170 | 171 | 172 | 173 | 174 | 175 | 176 | 177 | 178 | 179 | 180 | 181 | 182 | 183 | 184 | 185 | 186 | 187 | 188 | 189 | 190 | 191 | 192 | 193 | 194 | 195 | 196 | 197 | 198 | 199 | 200 | 201 | 202 | 203 | 204 | 205 | 206 | 207 | 208 | 209 | 210 | 211 | 212 | 213 | 214 | 215 | 216 | 217 | 218 | 219 | 220 | 221 | 222 | 223 | 224 | 225 | 226 | 227 | 228 | 229 | 230 | 231 | 232 | 233 | 234 | 235 | 236 | 237 | 238 | 239 | 240 | 241 | 242 | 243 | 244 | 245 | 246 | 247 | 248 | 249 | 250 | 251 | 252 | 253 | 254 | 255 | 256 | 257 | 258 | 259 | 260 | 261 | 262 | 263 | 264 | 265 | 266 | 267 | 268 | 269 | 270 | 271 | 272 | 273 | 274 | 275 | 276 | 277 | 278 | 279 | 280 | 281 | 282 | 283 | 284 | 285 | 286 | 287 | 288 | 289 | 290 | 291 | 292 | 293 | 294 | 295 | 296 | 297 | 298 | 299 | 300 | 301 | 302 | 303 | 304 | 305 | 306 | 307 | 308 | 309 | 310 | 311 | 312 | 313 | 314 | 315 | 316 | 317 | 318 | 319 | 320 | 321 | 322 | 323 | 324 | 325 | 326 | 327 | 328 | 329 | 330 | 331 | 332 | 333 | 334 | 335 | 336 | 337 | 338 | 339 | 340 | 341 | 342 | 343 | 344 | 345 | 346 | 347 | 348 | 349 | 350 | 351 | 352 | 353 | 354 | 355 | 356